Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 21

A viga de aço tem uma tensão de flexão admissível σ a d m = 140 M P a e a tensão de cisalhamento admissível τ a d m = 90   M P a . Determine a carga máxima que ela pode suportar com segurança.

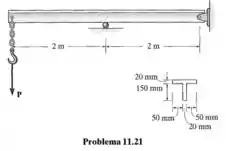
Passo 1

Dados da questão: σ a d m = 140 M P a , τ a d m = 90   M P a , L = 4   m , t = 20   m m , h = 150   m m , a = 50   m m , b = 120   m m

A questão pede: P = ?

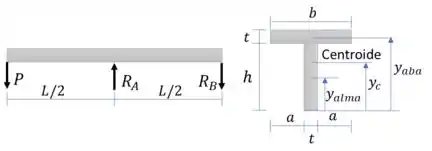
Para calcular a resistência da viga, vamos calcular a maior força P que pode ser aplicada sem ultrapassar as tensões admissíveis em flexão e cisalhamento. Para isso vamos precisar calcular as reações de apoio e os diagramas de esforços. Depois calcularemos as propriedades geométricas para que possamos aplicar as equações de flexão e de cisalhamento: centroide, momento de inércia e momento estático máximo.

Por fim, aplicamos a equação da flexão e do cisalhamento com as tensões admissíveis.

Passo 2

Vamos começar com as reações de apoio:

∑ M B = 0 ⇒ P ⋅ L - R A ⋅ L 2 = 0

R A = 2 P

∑ F Y = 0 ⇒ - P + R A - R B = 0

R B = P

Passo 3

Vamos utilizar a tabela 6.1 para gerar os diagramas de esforço cortante e momento fletor pelo método gráfico

M m a x = - P L 2

V m a x = P

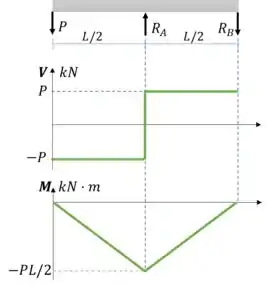
Passo 4

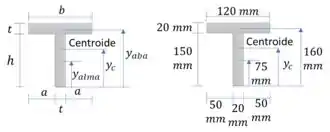
Vamos agora determinar o centroide da seção:

y c = b ⋅ t ⋅ y a b a + t ⋅ h ⋅ y a l m a b ⋅ t + t ⋅ h

y c = 20 ⋅ 120 ⋅ 160 + 20 ⋅ 150 ⋅ 75 20 ⋅ 120 + 20 ⋅ 150

y c = 112,78   m m

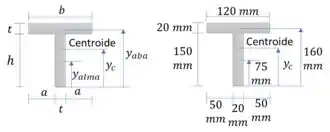
Passo 5

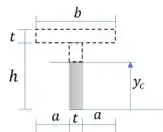
Calculamos o momento de inércia:

I = I a b a + I a l m a

I = b ⋅ t 3 12 + b ⋅ t ⋅ y a b a - y c 2 + t ⋅ h 3 12 + t ⋅ h ⋅ y c - y a l m a 2

I = 120 ⋅ 20 3 12 + 120 ⋅ 20 ⋅ 47,22 2 + 20 ⋅ 150 3 12 + 20 ⋅ 150 ⋅ 37,78 2

I = 15,34 ⋅ 10 6   m m 3

Passo 6

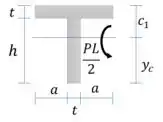
E calculamos também o momento estático máximo. Para isso vamos calcular o momento estático de toda a área abaixo do centroide:

Q = y c ⋅ t ⋅ y c 2

Q = 112,78 ⋅ 20 ⋅ 112,78 2

Q = 127193,284   m m 3

Passo 7

Vamos aplicar a equação da flexão. Vamos aplicar na distância y c pois é o ponto mais distante do centroide.

σ a d m = M ⋅ y c I

σ a d m = P L 2 ⋅ y c I

P L 2 = σ a d m I y c

P = 2 σ a d m I y c L

P = 2 ⋅ 140   M P a ⋅ 15,34 ⋅ 10 6   m m 4 112,78   m m ⋅ 4   m

P = 9521,19   N

Passo 8

Agora vamos testar a viga sobre cisalhamento

τ = V Q I t

τ = P Q I t

P = τ ⋅ I ⋅ t Q

P = 90   M P a ⋅ 15,34 ⋅ 10 6 m m 4 ⋅ 20   m m 127193,284   m m 3

P = 217086,93   N

Passo 9

Para garantir que a viga resista as duas condições, escolhemos o menor esforço

P = 9,52   k N

Resposta

P = 9,52   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a localização do centro de cisalhamento O da viga de parede fina com espessura uniforme, da seção transversal mostrada.
Determinar a localização do centro de cisalhamento O da viga de parede fina com a seção transversal mostrada.
Resolver o Prob. 5.122, considerando que a espessura da viga em balanço de parede fina é reduzida para 6,35m m .
A viga em balanço A B consiste de metade de um tubo de parede fina, com raio médio de 30m m e espessura da parede de 9,5m m . Sabendo-se que a carga vertical P passa através do centroide C da seção tr
Dois perfis laminados de aço W 130 × 23.8 podem ser soldados em A e B , de qualquer uma das três maneiras mostradas, para formar uma viga composta. Sabendo-se que para cada uma das soldas a força cisa