Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 36

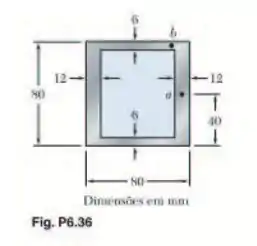
Uma viga de alumínio extrudada tem a seção transversal mostrada na figura. Sabendo que a força cortante vertical na viga é 150 kN, determine a tensão de cisalhamento no (a) ponto a e (b) ponto b.

Passo 1

Beleza! Precisamos encontrar a tensão de cisalhamento no ponto a e no ponto b, e nós sabemos que a tensão de cisalhamento é dada por:

τ = V Q I t

Em que V é a força cortante dada no enunciado, Q é o momento de área, I é o momento de inércia e t é a espessura da seção em análise, que pegamos através da figura dada no enunciado.

Passo 2

Tá legal! Vamos começar esse exercício calculando o momento de inércia da seção. Como temos uma seção vazada, podemos calcular o momento da seção considerando ela maciça e depois retirando a parte vazada. Sendo assim, nosso momento de inércia será:

I = b e h e 3 12 - b i h i 3 12

Em que o subscrito “e” se refere as medidas externas e o “i” se refere as medidas internas. Então, substituindo os valores conhecidos, teremos:

I = 0,08 0,08 3 12 - 0,08 - 2 0,012 0,08 - 2 0,006 3 12 → I = 1,946 . 10 - 6   m 4

Agora precisamos encontrar o momento de área para o ponto a. Nesse caso, vamos pegar a seguinte área para análise:

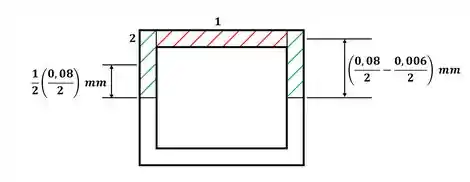
Então, sabendo que o momento de área é dado por:

Q = A y -

No nosso caso, para o ponto a, teremos:

Q a = A 1   y - 1 + 2 A 2 y - 2

Substituindo os valores conhecidos, chegamos em:

Q a = { 0,08 - 2 0,012 0,006 0,08 2 - 0,006 2 + 2 0,012 0,04 1 2 0,08 2

Q a = 12,432 . 10 - 6 + 19,2.10 - 6

Q a = 31,632 . 10 - 6   m 3

Agora, sabendo que a espessura da nossa área de interesse no ponto “a” será dada por:

t a = 2 0,012 → t a = 0,024   m

Agora podemos utilizar a equação da tensão de cisalhamento, dada por:

τ = V Q I t

E, substituindo os valores conhecidos para o ponto “a”, temos:

τ a = 150.10 3 31,632 . 10 - 6 1,946 . 10 - 6 0,024 → τ a = 101,6   M P a

Opa! Esse é o valor da tensão no ponto “a”, agora vamos para a letra (b).

Passo 3

Agora, para a letra (b), vamos destacar a área de interesse no ponto b, dada por:

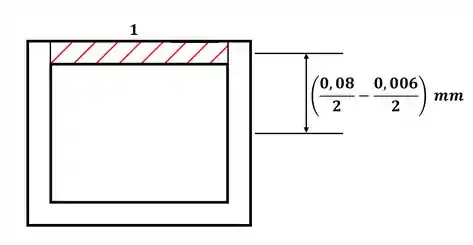
Note que já destacamos a distância entre o centroide da seção 1 e o centroide da viga. Dessa forma, nosso momento de área será:

Q b = { 0,08 - 2 0,012 0,006 0,08 2 - 0,006 2

Q b = 12,432 . 10 - 6

Agora, sabendo que a espessura da nossa área de interesse no ponto “b” será dada por:

t b = 2 0,006 → t b = 0,012   m

Agora podemos utilizar a equação da tensão de cisalhamento, dada por:

τ = V Q I t

E, substituindo os valores conhecidos para o ponto “b”, temos:

τ b = 150.10 3 12,432 . 10 - 6 1,946 . 10 - 6 0,012 → τ b = 79,9   M P a

E esse é o valor pedido na letra (b). Finalizamos por aqui!

Resposta

a : τ a = 10,6   M P a

b : τ b = 79,9   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
A viga mostrada na figura suporta uma força concentrada P e seu centro. Se for feita de uma chapa com largura constante b , determine a tensão de flexão máxima absoluta na viga
A viga com avanço foi construída com duas peças de madeira de 50 mm por 100 mm escoradas como mostra a figura. Se a tensão de flexão admissível for σ a d m = 4,2M P a , determine a maior carga P que p
Determine a variação do raio r da viga em balanço que suporta a carga distribuída uniforme, de modo que ela tenha uma tensão de flexão máxima constante σ m á x á em todo o seu comprimento.
A viga tem largura w e altura que varia como mostra a figura. Se ela suportar uma força concentrada P em sua extremidade, determine a tensão de flexão máxima absoluta na viga e especifique sua localiz