Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 124
Para a viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão na extremidade D. Usar .
Passo 1
Então galerinha, esse exercício é bem tranquilo, podemos usar o nosso conceito de sobreposição de cargas, essa sobreposição ocorre da seguinte maneira, podemos dividir cada uma das nossas cargas em uma viga separa, assim, temos que:
E a tabela que temos no fim do livro é dado por:
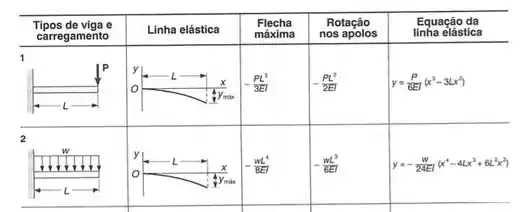
Sabemos que para a barra com a carga concentrada, podemos calcular a seguinte deformação e a inclinação no ponto D:
E para a barra com carga distribuída, precisamos ver que não temos a equação exata para o ponto D, mas podemos usar a nossa equação exatamente até o ponto B e depois, a partir do ponto B, podemos chegar no ponto D, assim, temos que:
Usando a distância de A até B como “a”, teremos que:
E olhando o ângulo em B, teremos que:
Mas como queremos o que rolou no ponto D, podemos fazer as seguintes aproximações:
E a deformação em D, considerando a distância entre B e D como “b”, teremos que:
Assim tem-se que:
Tendo isso em mãos, podemos ir para o próximo passo.
Passo 2
Queremos a deformação total em D, assim, é só somar as duas deformações que obtemos ali em cima para o ponto D.
E para o ângulo temos que:
Assim, olhando para o nosso problema, temos os seguintes valores numéricos:
Substituindo, temos que: