Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas de Revisão - Ex. 164
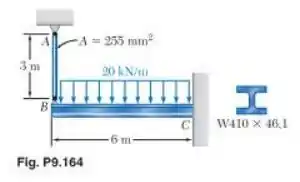
A viga em balanço é conectada ao cabo de aço conforme mostrado. Sabendo que o cabo inicialmente está esticado, determine a tensão no cabo causada pela ação distribuída mostrada. Utilize .
Passo 1
Fala aí, galera. Beleza? Vamos praticar mais mecânica pra tirar aquele na prova.
Primeiro, vamos chamar de a tensão desenvolvida no cabo e a sua variação. Temos que:
Para a viga , temos que o momento de inercia é tabelado para este perfil, e dado por:
Com isso, vamos dividir em casos de superposição para a viga inferior. O primeiro corresponde ao caso do nosso livro. Portanto:
Subsitituindo:
Para o segundo carregamento, temos o caso . Portanto:
Passo 2
Com isso, podemos encontrar a força . Vamos utilizar a seguinte relação
E também, a deflexão em é dada pela soma das deflexões dos casos de superposição. Logo: