Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 34
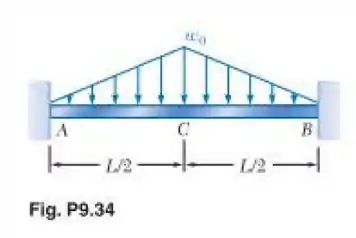
Determine a reação em A e desenhe o diagrama do momento fletor para a viga e o carregamento mostrados nas figuras.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar a equação que governa a linha elástica, dada por:
Então, nós precisamos da equação para o momento da viga, vamos determinar essa equação em função das reações nos apoios e depois integrar a equação acima duas vezes e utilizar as condições de contorno que temos para encontrar os valores das constantes, depois disso conseguimos obter a expressão para o momento fletor. Então bora lá!
Passo 2
Beleza! Vamos começar desenhando o DCL para o sistema, onde teremos:
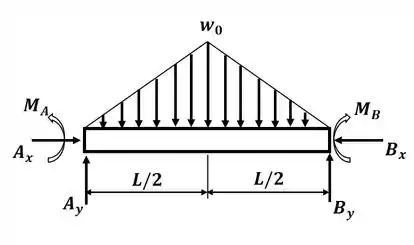
Agora nós vamos escrever a equação para o carregamento da viga, tomando o ponto A como início, sabendo que o carregamento equivale ao oposto da derivada da equação do cisalhamento, então teremos:
Agora vamos integrar essa equação, chegando em:
Nesse caso, a constante representa as forças localizadas que temos no sistema. Como escolhemos o ponto A como referência, só teremos a força , já que que está na outra extremidade não entra na equação. Dessa forma, nossa constante será:
E então a equação para o cisalhamento se torna:
Para obter o valor de , vamos utilizar a condição de contorno que temos no centro da viga, onde sabemos que não há força de cisalhamento, ou seja:
Substituindo esses valores na expressão para o cisalhamento, temos:
Então nossa equação para o cisalhamento será:
Passo 3
Agora, nós sabemos também que a derivada da equação do momento corresponde a equação do cisalhamento, podemos escrever:
Substituindo a expressão encontrada para o cisalhamento no passo 2, teremos:
Integrando essa equação, teremos:
Nesse caso, a constante representa os momentos localizados que temos no sistema. Como escolhemos o ponto A como referência, só teremos o momento , já que que está na outra extremidade não entra na equação. Dessa forma, nossa constante será:
E então a equação para o momento se torna:
Agora nós vamos utilizar a equação que governa o regime elástico, dada por:
Substituindo a expressão encontrada para o momento, chegamos em:
Passo 4
Agora nós vamos integrar a expressão obtida no passo 3, chegando em:
Essa será a equação para a inclinação da viga. Para descobrir o valor de vamos utilizar a nossa equação de contorno no engaste A, onde sabemos que não temos inclinação, ou seja:
Substituindo esses valores na equação de cima, teremos:
E a nossa equação para a inclinação será:
Agora nós vamos integrar essa expressão para obter a expressão para a deflexão da viga, onde teremos:
Passo 5
Agora, vamos utilizar a condição de contorno no engaste em A, onde sabemos que não há deflexão, ou seja:
Substituindo esses valores na equação anterior, temos:
Então a equação para a deflexão se torna:
Agora, para descobrir a equação para o momento fletor escrita no passo 3, falta somente a expressão para . Podemos obter esse valor sabendo que no meio da viga, não teremos inclinação, ou seja:
Então, substituindo esses valores na equação para a inclinação obtida no passo 4, teremos:
Então, nossa equação para o momento será dada por:
Feshoow! Era ela que a gente estava procurando!