Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 86

A viga balanço AB, consistindo de um tubo de paredes finas com raio médio de 31,8   m m e espessura de parede de 6,35   m m . está submetida passa a uma força vertical de 2224   k N . Sabendo que a linha de ação da força passa pelo centróide C da seção transversal da viga,determine (a) o sistema equivalente de força e momento no centro de cisalhamento da seção transversal e (b) a tensão de cisalhamento máxima na viga.(Sugestão:No problema 6.74, mostra-se a posição do centro de cisalhamento O ,distante em relação ao diâmetro vertical,do equivalente ao dobro da distância desse diâmetro ao centróide C.)

Passo 1

Então gurizada, o enunciado pede que a gente determine o sistema equivalente de força e momento no centro de cisalhamento da seção transversal e a tensão de cisalhamento máxima na viga. Vamos começar pelo esboço e depois fazer algumas conversões para facilitar nossos cálculos?!

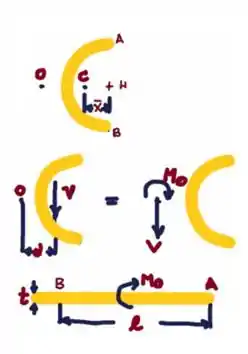
31,8   m m = 1,25   i n 6,35   m m = 1 / 4   i n 2224   k N = 500   l b

Agora, vamos iniciar nossos cálculos, temos as seguintes equações para correlacionar :D

I = π a 3 t Q = a 2 t   s i n θ e = 4 π a Q t o t a l = a 2 t

Para a seção do meio do tubo, a distância do centro do semicírculo até o centro é:

x _ = 2 π a

Em cada seção da viga, a força de cisalhamento V é igual a P. Sua linha de a ação passa pelo centróide C. O braço e momento de seu momento sobre o centro de cisalhamento O é:

d = e - x _ = 4 π a - 2 π a = 2 π a

Passo 2

Agora podemos encontrar o sistema de força em par equivalente em O, considerando que:

V = P M O = V d = 2 π P a

Tendo os dados a seguir, basta calcular:

P = 500   l b a = 1,25   i n

V = 500   l b = 2224   k N

M O = 2 x 500 π = 3 98   l b ⋅ i n =   180,53   k g / c m 3

Passo 3

Agora vamos determinar a tensões de cisalhamento, considerando que:

τ V = V Q t o t a l I t

τ V = ( P ) ( a 2 t ) ( π 2 a 3 t ( t ) ) = 2 P π a t = ( 2 ) ( 500 ) π ( 1,25 ) ( 0,250 ) = 1019   p s i

Devido ao torque M O :

Para uma seção retangular longa de comprimento de largura t, a tensão de cisalhamento devido ao torque é:

τ M = M O c 1 l t 2 onde c 1 = 1 3 1 - 0,630 t l

Passo 4

Temos então os seguintes dados:

l = π a = π ( 1,25 ) = 3,927   i n t = 0,250   i n c 1 = 0,31966

Agora basta aplicarmos na equação definida no passo anterior :D

τ m = 397,9 ( 0,31966 ) ( 3,927 ) ( 0,250 ) 2 = 5067   p s i

Por superposição temos:

τ = τ V + τ M = 1019   p s i + 5067   p s i

τ = 6090   p s i = 41.989 × 10 - 3   k P a

Resposta

(a) V = 500   l b = 2224   k N e M O = 398   l b ⋅ i n =   180,53   k g / c m 3

(b) τ = 6090   p s i = 41.989 × 10 - 3   k P a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga composta é feita de aço A-36 (A) unido a latão vermelho C83400 (B) e tem seção transversal mostrada na figura. Se a tensão de flexão admissível para o aço for (σadm)aço = 180 MPa e para o latão
Três pranchas são pregadas juntas de modo a formar a viga mostrada, a qual está submetida a uma força cortante vertical. Sabendo que o espaçamento entre os pregos é s = 75m m e a força cortante admiss
Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante
Uma viga de paredes finas de espessura uniforme tem a seção transversal mostrada na figura. Determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto