Três tábuas, cada uma com 50,8 mm de espessura, são pregadas entre si para formar uma viga que está submetida a uma força cortante vertical. Sabendo que a força cortante admissível em cada prego é de 667 N, determine a força cortante admissível se o espaçamento s entre os pregos for de 76,2 mm.
Passo 1
Galerinha, o enunciado pede que a gente determine a força cortante admissível, então considere o esboço a seguir:
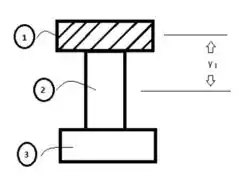
A inércia do elemento foi dividida em 3 partes para determinarmos, então partiu!
Passo 2
Então começaremos calculando a inércia 1;
Para a inércia 2 temos:
E a inércia 3 temos:
inércia total é a soma de todos:
(1)
Dividindo Eq. (2) por Eq. (1),
Resposta
.