Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 26

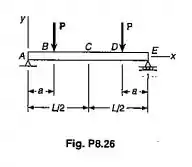
Para a viga com o carregamento mostrado, determinar: (a) a equação da linha elástica para a porção B D ;   (b) a declividade em B ; (c) a deflexão no centro C   da viga.

Passo 1

Fala aí galera. Bora estudar resmat.

O primeiro passo para este tipo de questão é calcular a equação do momento. Sabemos que:

E I d y 2 d 2 x = M x

Por simetria, sabemos que as reações nos apoios serão iguais a P . Se estiver com dúvida, faz as equações de equilíbrio, mas pode confiar. Logo, a equação do momento em BD será:

M x = F A x - P x - a = P x - P x + P a = P a

Portanto:

E I d y 2 d 2 x = P a

d y 2 d 2 x = P a E I

Esta é a equação da linha elástica.

Passo 2

Para a letra b, devemos integrar a função da linha elástica e substituir o ponto pedido. Logo:

E I d y d x = θ = P a x + C 1

Esta é a declividade em função da distância x .

Agora, derivamos outra vez para que possamos achar a deflexão.

E I y = P a x 2 2 + C 1 x + C 2

Note que temos 2 constantes, que surgem na integração. Para eliminá-las, usaremos as condições de contorno:

x = 0 → θ = 0   e   y = 0 → C 1 = C 2 = 0

Passo 3

Agora, basta substituir os dados pedidos nas equações:

E I θ x = P a x

θ a = P a 2 E I

E I y x = P a x 2 2

y L 2 = P a L 2 8 E I

Resposta

  1. d y 2 d 2 x = P a E I
  2. θ a = P a 2 E I
  3. y L 2 = P a L 2 8 E I
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a reação em A e desenhe o diagrama do momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados nas figuras, determine (a) a equação da linha elástica, (b) a inclinação na extremidade A e (c) a deflexão do ponto C.
Para o carregamento mostrado nas figuras, determine (a) a equação da linha elástica para a viga em balanço AB, (b) a deflexão da extremidade livre e (c) a inclinação na extremidade livre.
Determine a reação em A e desenhe o diagrama do momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A, (b) a deflexão no ponto B e (c) a deflexão na extremidade D.