Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 42
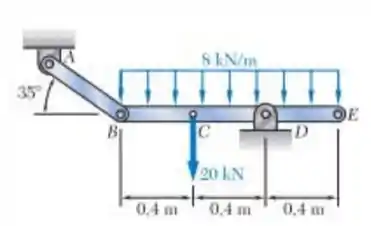
O vínculo AB deve ser feito de aço para o qual a tensão normal é de 450 MPa. Determine a área da seção transversal da AB para a qual o fator de segurança será 3,50. Suponha que o vínculo seja reforçado adequadamente ao redor dos pinos em A e B
Passo 1
E aiii.. belezinha???
Nessa questão vamos usar a relação pra achar a área transfersal de AB:
Daí a gente vai precisar do diagrama de corpo livre pra achar . Então já vamos montar essa bagaça.
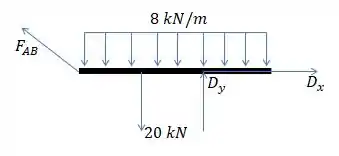
Passo 2
Maaaas como a gente só quer achar as forças e tals, a gente pode multiplicar essa carga distribuída pela distância de B até E e considerar uma carga localizada bem no meio, sacou?
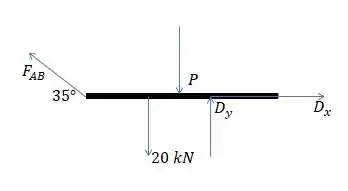
Então essa carga vai ser:
E vai estar bem no meiozinho, entre BE. (que vai ser igual a , já que a gente vai escolher o ponto D pra fazer o balanço, como espoiler)
Passo 3
Vamos, então fazer o balanço de momento em D (já que queremos achar só o , né):
Com o sentido anti-horário positivo:
Passo 4
E agora vamos jogar na relação:
Aiiii... namoralzinha... vamos arrumar as unidades pra gente não errar bobeira, ta bém??
E o fator de segurança é adimensional, né...
Agora sim, jogando na relação:
Ps: no livro que a gente usou a resposta lá atrás está errada.