Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 111d
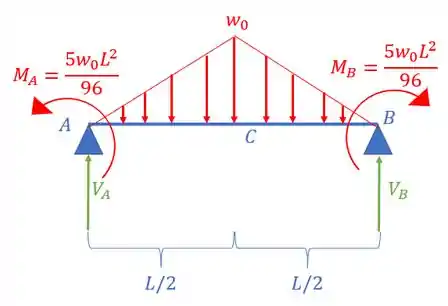
Para a viga com o carregamento mostrado, determinar:
- O momento fletor na extremidade A
Obs: determinação da reação em A para o caso 4
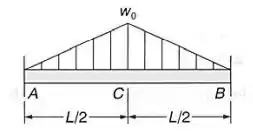
Passo 1
Agora temos que tomar o seguinte cuidado, sabemos que temos 3 casos de vigas, e para cada um dos casos determinamos os ângulos nos seus apoios, e assim obtivemos o seguinte:
- Caso 1
- Caso 2
- Caso 3
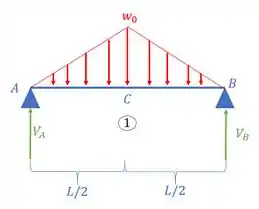
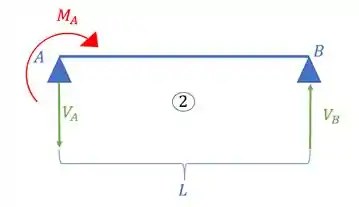
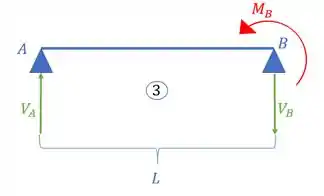
Com isso em mãos, precisamos lembrar o seguinte, cada apoia é um engaste, logo, a soma dos ângulos em cada apoio representa esse engaste, ou seja, essa soma tem que dar zero, assim podemos dizer que:
Assim obtém-se o seguinte sistema:
Isolando , obtém-se que:
Na segundo equação, multiplicando em cima e embaixo por 2, obtém-se que:
E substituindo a segunda equação, obtém-se que será:
Passo 2
Como descobrimos os momentos, podemos determinar a reação de apoio vertical, lembrando que como os momentos nas extremidades das vigas deram negativos, vamos inverte-los com o intuito de usar valores positivos no nosso problema.
