Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 102a

Para a viga com o carregamento mostrado, determinar:

  1. A reação em A

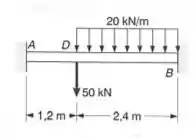
Passo 1

Para usarmos as funções singulares, podemos girar a nossa seção, e fazermos uma mudança para facilitar o nosso cálculo, assim, podemos trabalhar com a seguinte viga:

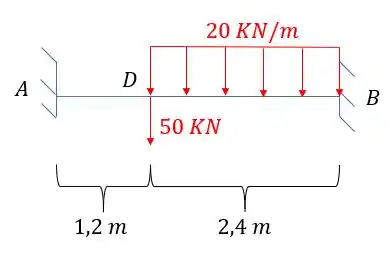
Separando por regiões temos:

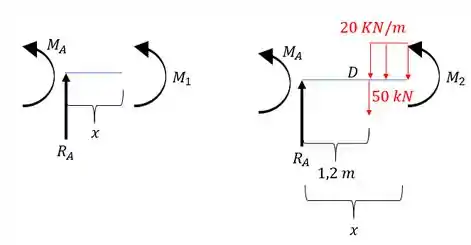
Assim temos que os momentos vão ser dados por:

M 1 = R A x - M A

M 2 = R A x - M A - 50 < x - 1,2 > - 20 2 < x - 1,2 > 2

E assim podemos definir o nosso momento fletor como sendo:

M x = R A x - M A - 50 < x - 1,2 > - 20 2 < x - 1,2 > 2

E esse momento que iremos usar na nossa equação, então vamos porá o próximo passo.

Passo 2

Sabemos que a equação que iremos relacionar a integração é dada por:

E I d 2 y d x 2 = M x = R A x - M A - 50 < x - 1,2 > - 20 2 < x - 1,2 > 2

Integrando duas vezes teremos que:

E I θ = R A x 2 2 - M A x - 50 2 < x - 1,2 > 2 - 20 6 < x - 1,2 > 3 + C 1

E I y = R A x 3 6 - M A x 2 2 - 50 6 < x - 1,2 > 3 - 20 24 < x - 1,2 > 4 + C 1 x + C 2

E sabemos que as condições de contorno vão ser dadas por:

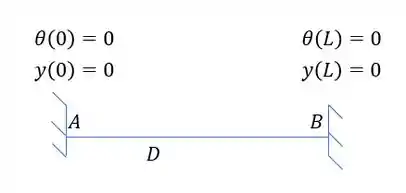
E assim podemos descobrir as nossas incógnitas.

Passo 3

Olhando cada uma das condições de contorno, vamos ter que:

  • y 0 = 0

    • Para o ponto inicial, consideramos as equações singulares iguais a zero por elas não estarem no intervalo que estamos, assim, podemos determinar que:

    E I y = R A x 3 6 - M A x 2 2 - 50 6 < x - 1,2 > 3 - 20 24 < x - 1,2 > 4 + C 1 x + C 2

    0 = R A 0 3 6 - M A 0 2 2 + C 1 0 + C 2

    C 2 = 0

  • θ 0 = 0

    • Para o ponto inicial, consideramos as equações singulares iguais a zero por elas não estarem no intervalo que estamos, assim, podemos determinar que:

    E I θ = R A x 2 2 - M A x - 50 2 < x - 1,2 > 2 - 20 6 < x - 1,2 > 3 + C 1

    0 = R A 0 2 2 - M A 0 + C 1

    C 1 = 0

  • θ L = 3,6 = 0

    • Aqui usamos a equação inteira, assim vamos ter que:

    E I θ = R A x 2 2 - M A x - 50 2 < x - 1,2 > 2 - 20 6 < x - 1,2 > 3 + C 1

    0 = R A 3,6 2 2 - M A 3,6 - 50 2 ( 3,6 - 1,2 ) 2 - 20 6 ( 3,6 - 1,2 ) 3

    0 = 6,48 R A - 3,6 M A - 144 - 46,08

    M A = 1,80 R A - 52,8

  • y L = 3,6 = 0

Aqui usamos a equação inteira, assim vamos ter que:

E I y = R A x 3 6 - M A x 2 2 - 50 6 < x - 1,2 > 3 - 20 24 < x - 1,2 > 4 + C 1 x + C 2

0 = R A 3,6 3 6 - M A 3,6 2 2 - 50 6 ( 3,6 - 1,2 ) 3 - 20 24 ( 3,6 - 1,2 ) 4

0 = 7,776 R A - 6,48 M A - 115,2 - 27,648

M A = 1,2 R A - 22,04

Igualando os dois momentos temos que:

1,2 R A - 22,04 = 1,80 R A - 52,8

R A = 51,3   k N

Para acharmos o momento, basta substituirmos, assim temos que:

M A = 1,80 R A - 52,8 = 1,80 × 51,3 - 52,8 = 39,5   k N m

Resposta

  1. R A = 51,3   k N             ;           M A = 39,5   k N m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tábua de cerca está entrelaçada entre os três mourões lisos fixos. Se os mourões estiverem instalados ao longo da mesma linha reta, determine a tensão de flexão máxima na tábua. A largura e a espess
Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a inclinação em A . E I é constante.
Para a viga em balanço e o carregamento mostrados, determine ( a ) a inclinação no ponto A , ( b ) a deflexão no ponto A . Utilize E = 200G P a .
Para o carregamento mostrado, determine ( a ) a equação da linha elástica para a viga em balanço A B , ( b ) a deflexão da extremidade livre e ( c ) a inclinação na extremidade livre.
Para a viga e o carregamento mostrados na figura, determine ( a ) a equação da linha elástica, ( b ) a inclinação na extremidade A e ( c ) a deflexão no ponto médio do vão livre.