Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas de Revisão - Ex. 157
Para o carregamento mostrado, determine a equação da linha elástica para a viga em balanço , a deflexão da extremidade livre e a inclinação na extremidade livre.
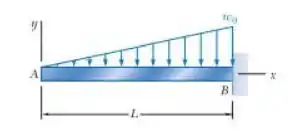
Passo 1
Fala aí, pessoal. Tudo certo? Bora fazer mais um exercício pra ficar craque.
Primeiro, vamos considerar a reação no ponto como redundante e esboçar o DCL para este caso, temos:
Em seguida, vamos utilizar a equação de momento no ponto para determinarmos a equação para o momento fletor:
Com isso, podemos substituir esta equação que encontramos na equação diferencial da linha elástica. Ela é dada por:
Substituindo:
Agora, considerando a rigidez à flexão constante, vamos integrar esta equação duas vezes, para obtermos, respectivamente, a equação para a força cortante e a equação da linha elástica. Integrando, temos:
Integrando mais uma vez:
Passo 2
O próximo passo para encontrarmos a equação da linha elástica é determinarmos as constantes. Para isso, vamos utilizar as condições de contorno. São elas:
Ou seja, quando está no ponto , a força cortante é nula. E também, no mesmo ponto, a equação para linha elástica é igual a . Com isso, vamos substituir estas condições nas respectivas equações para determinarmos as constantes. Para a primeira:
E para a segunda condição, temos:
Com as constantes definidas, basta as substituirmos na equação que encontramos anteriormente. Fica assim:
Esta é a nossa equação para a linha elástica.
Passo 3
Em seguida, para determinarmos a deflexão da extremidade livre basta utilizarmos a equação para a linha elástica que encontramos no item anterior e substituirmos no ponto em que a extremidade está livre, neste caso, em . Assim, substituindo:
Passo 4
Por fim, para determinarmos a a inclinação na extremidade livre vamos utilizar a equação para a força cortante e substituirmos no ponto indicado. Neste caso, em . Portanto:
É isso, galera! Vamos fazer mais questões.