Para a viga e o carregamento mostrados, considere a seção n-n e determine (a) a maior tensão de cisalhamento naquela seção e (b) a tensão de cisalhamento ao ponto a.
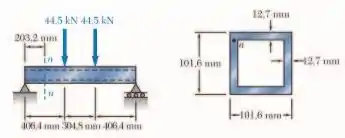
Passo 1
Falaaaa... belezinha?
Nessa questãozinha usar o balanço de forças verticais:
E pra a tensão de cisalhamento usamos:
E mais umas coistinhas, mas vamos apresentando ao longo da questão, ok?
Passo 2
Já vamos começar reparando que tem uma simetria marota, né?? Com isso vamos ter:
E fazendo o balanço de forças:
E montando o diagrama de força cortante:
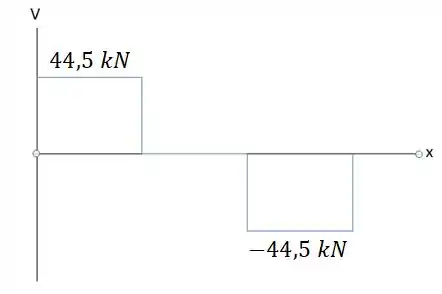
Daí podemos tirar:
Passo 3
Agora vamos calcular o momento de inércia, mas repara na imagem:
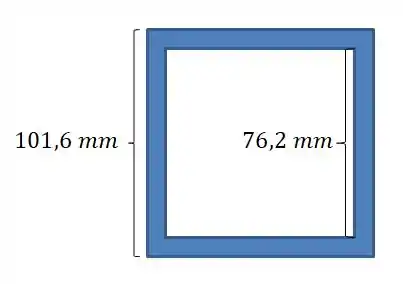
A gente imagina que a seção é um quadradão preenchido azul, de lado ( e ), e tira o quadrado branco, de lado ( e , certo?
Daí fica:
Passo 4
- Para calcular o Q:
- Para calcular a tensão no ponto :
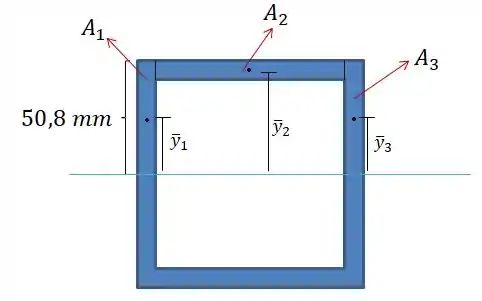
Então:
E só falta o pra podermos jogar na equação e achar a tensão máxima, né?
Agora sim podemos colocar na equação:
Passo 5
E para :
Jogando na equação:
Ufaa... acabamos... Bora pra próxima???