Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas de Revisão - Ex. 155
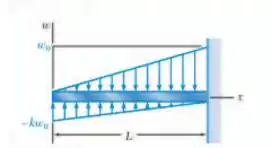
Para a viga e o carregamento mostrados, determine as equações das curvas de força cortante e momento fletor e o valor absoluto do momento fletor máximo na viga, sabendo que , .
Passo 1
Fala aí, pessoal. Tudo certo? Bora zerar esse livro.
Primeiro, precisamos identificar em qual caso o carregamento se enquadra. Podemos ver que o carregamento é dado pela seguinte função:
O próximo passo é integrar a função para o carregamento a fim de obtermos a equação para força cortante. Fica assim:
Pelas condições de contorno, temos que em :
Essa é a equação para a força cortante. Bora para a equação do momento fletor. Para a encontrarmos precisamos integrar a equação de força cortante, temos:
Pelas condições de contorno, temos que em
Passo 2
Agora que encontramos a equação para o momento fletor, podemos encontrar o momento fletor máximo. Vale lembrar que o enunciando nos diz que , logo nossas equações serão:
E então, sabemos que o momento fletor máximo ocorre em , portanto, substituindo na equação que a gente achou, temos:
Passo 3
Em seguida, o problema nos pede para repetir o processo mas agora com . Substituindo, nossas equações para o momento fletor e força cortante serão:
Desta vez, o momento fletor máximo, ou seja, quando , ocorre em , logo:
Opa, é isso, pessoal.