Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 1
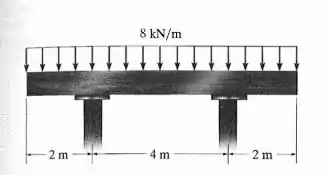
A viga simplesmente apoiada é feita de madeira com tensão de flexão admissível MPa e tensão de cisalhamento admissível = . Determine as dimensões da viga se ela tiver de ser retangular e apresentar relação altura/largura de 1,25.
Passo 1
Fala aí galera. Queremos dimensionar essa viga. Para isso, precisamos achar onde os esforços nela são máximos.
O primeiro passo deste problema é determinar as reações de apoio. Percebe que nossa estrutura e o carregamento s]ao simétricos.
A carga externa nela é
Por simetria, sabemos que as reações serão iguais e serão metade da carga externa. Então nossas reações são:
Passo 2
Vamos fazer os diagramas para determinarmos os esforços máximos atuantes. A gente pode usar o método gráfico da “viagem do cortante” para achar o diagrama do cortante.
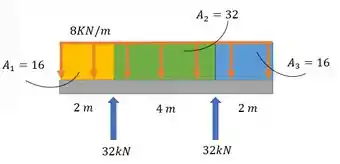
Como fuciona? A gente vai começar do zero, descer até o ponto onde , mas através de uma reta inclinada (por causa do carregamento distribuído).
Em , a gente sobe(sentido da força) reto o valor de (a força nesse ponto). Depois dessa a gente desce o valor da área , até o ponto onde . Usamos uma reta inclinada novamente.
Nesse ponto a gente sobe de novo. E volta a descer o valor de através de uma reta inclinada até o ponto onde Esse é o diagrama de cortante:
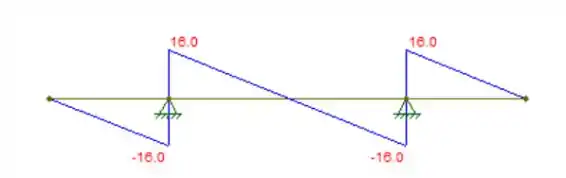
Vemos que o cortante máximo é
Passo 3
Para o diagrama dos momentos, nós calculamos o momento nos pontos críticos(extremidades e apoios). E ligamos esses pontos que achar por parábolas porque temos um carregamento distribuído.
Para saber a concavidade da parábola, vemos se a reta do cortante é crescente. Se for, a concavidade é para cima. Se não, a concavidade é para baixo.
Como aqui a gente usa a convenção de colocar o positivo do diagrama de momento na parte de baixo, para verificar essa questão da concavidade, cê olha para ele de cabeça para baixo haha Mas se você coloca a parte positiva em cima mesmo, fica tranquilo de ver.
O diagrama de momento fica:
Pelo diagrama, podemos ver que o momento máximo é
Passo 4
Agora, vamos aplicar a fórmula da flexão:
Mas temos também que:
Substituindo isso ali em cima:
Logo
Passo 5
Vamos considerar uma viga de largura e altura , porque o enunciado diz que a razão entre altura e largura é .
é a metade da altura da seção, onde ocorre o momento máximo em relação a seção:
E é o momento de inércia da seção retangular:
Substituindo o momento de inércia e o valor de c na nossa equação do passo anterior:
E como a gente quer as dimensões da seção da viga, a gente pode isolar :
A altura da seção é 1,25b, logo:
Passo 6
Vamos agora verificar se a tensão não ultrapassa a admissível para o cisalhamento. Vamos usar:
é o momento de inércia:
é a largura da seção, é o cortante máximo e é o momento estático da metade da nossa seção, isso porque o cisalhamento máximo na seção ocorre na metade dela. Aí é dado pelo produto entre metade da área da seção e um quarto da altura da seção:
Calculando cada uma dessas coisinhas sabendo que e substituindo na fórmulinha, a gente acha:
Logo, está ok, porque essa tensão é menor que a admissível de cisalhamento = .