Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 93
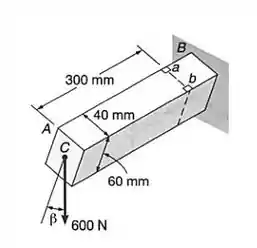
Para a viga e o carregamento do Prob , determinar: o valor de para que a tensão normal no ponto seja zero; a correspondente tensão normal no ponto .
Passo 1
Fala aí galera, bora para mais uma questão de Resmat. Primeiro, vamos calcular a força normal na direção da força que é aplicada no tubo (chamaremos de eixo ), temos:
Passo 2
Com isso, vamos encontrar o o valor de . Temos:
Passo 3
Agora, para calcularmos a tensão normal no ponto , temos:
Resposta
Exercícios de Livros Relacionados
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
Determine a localização e do centro de cisalhamento (ponto O ) para o elemento de paredes finas com a seção transversal mostrada na figura, onde b 2b 1 . Os segmentos do elemento têm a mesma espessura
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .