Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 128
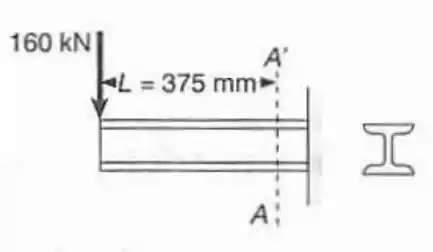
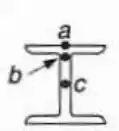
Para a viga e o carregamento do Prob. Resolvido 7.11, determinar a máxima tensão de cisalhamento nos pontos e .
Passo 1
Bom, primeiro vale lembrar que a viga do problema resolvido 7.11 é uma viga . Sabendo disso vamos resolver o problema seguindo o passo a passo:
- Calcular a força cortante na região
- Calcular a tensão de cisalhamento para cada ponto, por meio da seguinte equação:
obs: Os valores e são todos dados na tabela!
Passo 2
Vamos achar a força cortante na região utilizando a equação do momento para casos estáticos:
Passo 3
Agora vamos utilizar a nossa equação:
Primeiro para o ponto :
Olhando na tabela vemos que:
E o termo pode ser calculado como:
Substituindo na equação:
Passo 4
Agora para :
É importante perceber que todos os valores, exceto o permanecem constantes. Desta forma temos de calcular o novamente, que agora é dado por:
UAI!!
Isso mesmo, nas extremidades o nosso sempre vai ser nulo assim:
Passo 5
Agora para a linha neutra:
Novamente precisamos calcular apenas o :
Substituindo:
Resposta
a)
b)
c)