Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 1
O diâmetro de um balão de borracha cheio de ar é 150 mm. Se a pressão do ar em seu interior for aumentada até o diâmetro atingir 175 mm, determine a deformação normal média na borracha.
Passo 1
Falaaa! Ele quer a deformação normal média na borracha, ok? Vamos lembrar que a deformação normal média é dada por:
Onde é a diferença entre um comprimento final e um comprimento inicial numa direção do nosso elemento. E é o comprimento inicial.
Para esse caso, a gente pode pegar como comprimento o comprimento da borda de uma seção do balão (a parte que é feita da borracha). Assim:
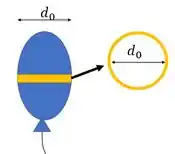
Aí a gente calcula para essa borda. Bora!
Passo 2
Chamemos o diâmetro inicial do balão de e o diâmetro após a deformação de . Temos
O comprimento da seção do balão fica:
Aí, a deformação normal média é dada por
Dessa forma, colocando em evidência no numerador poderemos simplificar com o presente no denominador e ficaremos com