Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 127
A viga de concreto armado é feita com duas hastes de reforço de aço. Se a tensão de tração admissível para o aço for (σaço)adm = 280 MPa e a tensão de compressão admissível apara o concreto for (σconc)adm = 21 MPa, determine o momento máximo M que pode ser aplicado a seção. Considere que o concreto não pode suportar uma tensão de tração.
E
aço
= 200 GPa, E
conc
= 26,5 GPa.
.
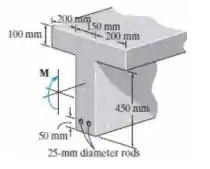
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questão de hoje nos traz uma viga composta por dois materiais diferentes, mas vou te explicar direitinho. Os materiais que compõem são o aço e o concreto, e ele nos pede para calcular os dois momentos máximos (tanto para o aço quanto para o concreto) e pegaremos o menor (afinal, se pegarmos o maior, o ‘’mais fraco’’ vai se romper com o momento do outro) para uma tensão admissível dada. Viu?? Ela só tem cara de malvada, mas vamos resolver rapidinho. Vem comigo!!
Passo 2
A primeira coisa que precisamos achar é a relação entre os coeficientes Econ e Eaço e a altura da nossa linha neutra.
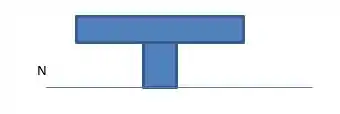
Passo 3
Agora que já temos nossas dimensões, podemos calcular o momento máximo da viga. Para isso, vamos calcular primeiro o nosso I, para só depois substituir na nossa formulinha.