Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 75
A viga é composta está fiada em A e é sustentada por apoios oscilantes em B e C. Existem dobradiças (pinos) em D e E. Determine as cmponentes da reação nesses suportes.
Passo 1
Podemos começar desenhando o diagrama do corpo livre (DLC) do elemento EC:
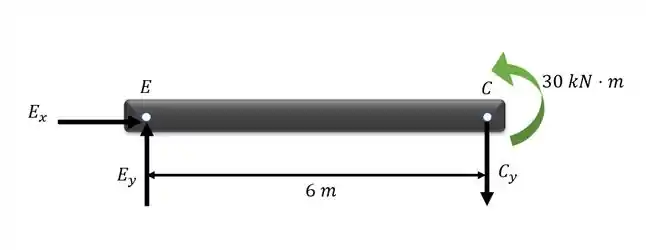
Agora podemos utilizar a equação do equilíbrio em relação ao momento para o ponto E. A força Cy causa momento no sentido horário e o mometo de 30 kNm dado causa momento horário. Portanto, podemos escrever:
Passo 2
Aplicando a equação do equilíbrio para o trecho EC na direção x:
Passo 3
Aplicando a equação do equilíbrio para o trecho EC na direção y:
Passo 4
Agora desenhamos o diagrama do corpo livre (DLC) do elemento DE:
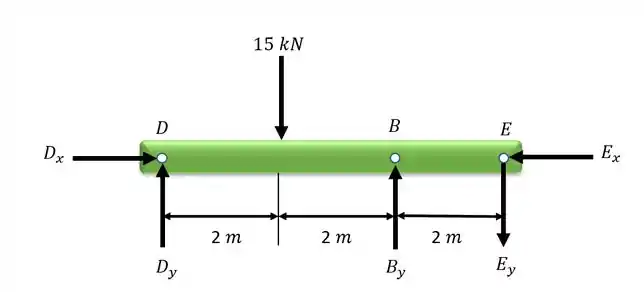
Agora podemos utilizar a equação do equilíbrio em relação ao momento para o ponto D. As forças Ey e a de 15 KN causam momento no sentido horário e e a força de 15 Kn causa momento anti-horário. Portanto, podemos escrever:
Passo 5
Aplicando a equação do equilíbrio para o trecho EC na direção x:
Passo 6
Aplicando a equação do equilíbrio para o trecho EC na direção y:
Substituindo e em :
Passo 7
Agora vamos desenhar o diagrama do corpo livre do corpo (DLC) do trecho AD:
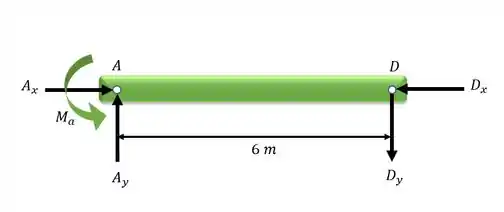
Agora podemos utilizar a equação do equilíbrio em relação ao momento para o ponto A. A Força Dy causa momento horário e o momento Ma causa momento anti-horário. Podemos escrever:
Passo 8
Aplicando a equação do equilíbrio para o trecho AD na direção x: