Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 85a
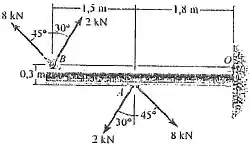
85. Determine o momento de binário resultante que age sobre a viga. Resolva o problema de duas maneiras;
(a) some os momentos em relação ao ponto .
Passo 1
Vamos começar fazendo o diagrama de corpo livre pra analisarmos isso melhor.
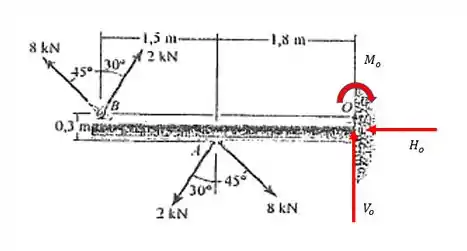
No nosso caso os esforços em O não são relevantes para o cálculo do momento binário, e também podemos desconsiderar os esforços horizontais em B pois passa pelo mesmo eixo de O.
Vamos calcular o momento binário usando a análise escalar:
Onde é a intensidade das forças e é a distância perpendicular ou braço de momento entre as forças.
Porém a força precisa ser perpendicular a distância, então vamos decompor em duas direções, porém a força no ponto B só necessita da componente vertical.
E para a força no ponto A, temos:
E para o eixo x
Passo 2
Enfim vamos ao calculo dos momentos por aqui meu povo, o momento no ponto O vai ser causado pelos dois binários, porém como a gente já viu a força horizontal de B não causa nenhum momento em O, então considerando o sentido horário positivo temos:
Onde
Resposta
O momento de binário é: