Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 20

A viga composta foi feita com duas seções unidas por um pino em B. Use o Apêndice B e selecione a viga de abas largas leve que seria segura para cada seção, se a tensão de flexão admissível for σ a d m = 168   M P a e a tensão de cisalhamento admissível for τ a d m = 100   M P a . A viga suporta a carga de um tubo de 6   k N e 9   k N , como mostra a figura.

Passo 1

Dados da questão: σ a d m = 168   M P a , τ a d m = 100   M P a

A questão pede pra selecionar uma viga apropriada.

Para resolver, vamos começar calculando as reações de apoio, como a viga tem um pino, vamos fazer uma seção neste ponto. Lembre-se que em um pino, o momento interno é igual a zero. Depois de calcular as reações de apoio, vamos traçar os diagramas de esforços interno.

Depois vamos testar a resistência da viga sobre flexão e cisalhamento para que possamos determinar uma viga apropriada para cada seção

Passo 2

Vamos separar a viga no pino, e calcular as reações de apoio.

Vamos analisar o lado direito primeiro:

∑ M C = 0 ⇒ - R B ⋅ 5,4 + 9 ⋅ 3 = 0

R B = 5   k N

∑ F y = 0 ⇒ R B - 9 + R C = 0

R C = 4   k N

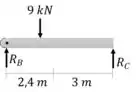
Analisando a outra seção da viga

∑ F y = 0 ⇒ R A - 6 - R B = 0

R C = 11   k N

∑ M B = 0 ⇒ M A - R A ⋅ 3,6 + 6 ⋅ 1,8 = 0

M A = 28,8   k N ⋅ m

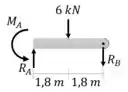
Passo 3

Utilizamos a tabela 6.1 do livro para utilizar o método gráfico para gerar os diagramas de esforço cortante e momento fletor.

V A B = 11   k N

M A B = - 28,8   k N ⋅ m

V B C = 5   k N

M B C = 12   k N ⋅ m

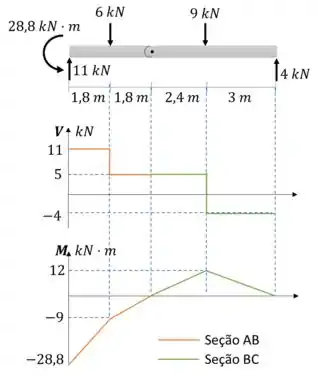
Passo 4

Vamos estudar cada uma das seções aplicando a equação 11.1 para testar a viga sobre flexão

  • Seção AB

    • S A B = M A B σ A B

    S A B = 28,8   k N ⋅ m 168   M p a

    S A B = 171,43 ⋅ 10 3   m m 3

    Pelo apêndice B podemos selecionar um perfil para a viga AB

    P e r f i l   A B ⇒   W 250 x 18 S W 250 x 18 = 178 ⋅ 10 3   m m 3 t a l m a W 250 x 18 = 4,83   m m d W 250 x 18 = 251   m m

  • Seção BC

    • S B C = M B C σ B C

    S B C = 12   k N ⋅ m 168   M p a

    S B C = 71,43 ⋅ 10 3   m m 3

    Pelo apêndice B podemos selecionar um perfil para a viga BC

    P e r f i l   B C ⇒   W 150 x 14 S W 150 x 14 = 91,2 ⋅ 10 3 m m 3 t a l m a W 150 x 14 = 4,32   m m d W 150 x 14 = 150   m m

    Passo 5

    Vamos testar a resistência ao cisalhamento de cada seção. Como são vigas de abas largas, podemos considerar apenas a área da alma da viga

  • Seção AB

    • τ A B = V A B t a l m a W 150 x 14 d W 150 x 14

    τ A B = 5   k N 4,32 m m ⋅ 150 m m

    τ A B = 11,44   M P a

  • Seção BC

τ B C = V B C t a l m a W 250 x 18 d W 250 x 18

τ B C = 11   k N 4,83 m m ⋅ 251 m m

τ B C = 7,72   M P a

A tensão de cisalhamento em ambas as vigas é bem abaixo da tensão admissível. Isso garante a resistência das vigas selecionadas

Resposta

S W 250 x 18 = 178 ⋅ 10 3   m m 3

S W 150 x 14 = 91,2 ⋅ 10 3   m m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob. 5.32, considerando que a dimensão t é aumentada para 7,6mm.
Para o perfil cantoneira e o carregamento mostrado no Prob. Resolvido 5.8, verificar que ∫ qd y = P , ao longo da perna vertical da cantoneira.
Para o perfil cantoneira e o carregamento mostrado no Porb. Resolvido 5.8, verificar que ∫ qd z = 0 , ao longo da perna horizontal da cantoneira.
Uma placa de aço de 160m m de largura e 8m m de espessura é dobrada para formar o perfil mostrado. Sabendo-se que a carga vertical P atua em um ponto localizado na superfície média da alma, determinar
Para o perfil cantoneira e o carregamento mostrado no Prob 5.8, pede-se: a determinar o pontos onde a tensão de cisalhamento é máxima e seus correspondentes valores de tensão; b verificar que os ponto