Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 22

A viga de madeira tem seção transversal retangular. Se sua largura for 150 mm, determine a altura h de modo que atinja simultaneamente sua tensão de flexão admissível σ a d m = 10   M P a e uma tensão de cisalhamento admissível τ a d m = 0,35   M P a . Calcule também a carga máxima P que a viga pode suportar.

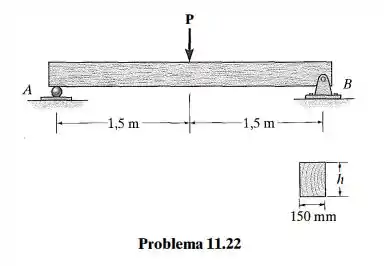
Passo 1

Dados da questão: b = 150   m m ,   σ a d m = 10 M P a ,   τ a d m = 0,35 M P a ,   L = 3 m  

A questão pede o valor P = ? e h = ? de forma que se atinja tensão admissível em cisalhamento e flexão.

Passo 2

Começamos pelas reações de apoio

∑ M B = 0 ⇒ R A L - P ⋅ L 2 = 0

R A = P 2

∑ F Y = 0 ⇒ R A - P + R B = 0

R B = P 2

Passo 3

Agora vamos gerar os diagramas de esforço cortante e momento fletor pelo método gráfico, seguindo a Tabela 6.1

V M a x = P 2

M m a x = - P L 4

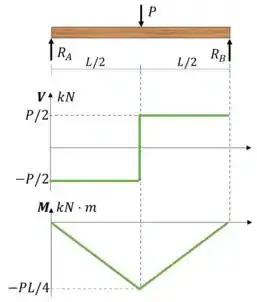
Passo 4

Vamos agora calcular as propriedades geométricas da seção. O momento de inércia é:

I = b h 3 12

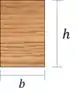
Passo 5

O momento estático é:

I = b ⋅ h 2 ⋅ h 4

I = b h 2 8

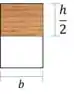
Passo 6

Vamos aplicar a equação da flexão.

σ a d m = M m a x ⋅ c I  

A distância c será igual a metade da altura. Vamos substituir as expressões na equação

σ a d m = P L 4 ⋅ h 2 b h 3 12

σ a d m = 12 b h 3 ⋅ P L 4 ⋅ h 2

σ a d m = 3 2 ⋅ P L b h 2

Isolando a altura h

h 2 = 3 P L 2 b ⋅ σ a d m

Passo 7

Vamos agora observar a equação do cisalhamento

τ a d m = V m á x Q I t

Aplicando as expressões:

τ a d m = P 2 b h 2 8 b h 3 12 ⋅ b

τ a d m = P 2 b h 2 8 12 b 2 h 3

τ a d m = 3 P 4 b h

Isolando a altura h :

h = 3 P 4 b ⋅ τ a d m

Passo 8

Chegamos a um sistema de equações de duas variáveis h e P .

h 2 = 3 P L 2 b ⋅ σ a d m h = 3 P 4 b τ a d m

Se substituirmos a segunda na primeira

3 P 4 b τ a d m 2 = 3 P L 2 b ⋅ σ a d m

9 P 2 16 b 2 τ a d m 2 = 3 P L 2 b σ a d m

Simplificando:

3 P 8 b τ a d m 2 = L σ a d m

P = 8 b τ a d m 2 L 3 σ a d m

Aplicando os valores, com as medidas já convertidas para milímetros e mega pascal

P = 8 ⋅ 150   m m ⋅ 0,35   M P a 2 ⋅ 3000   m m 3 ⋅ 10   M P a

P = 14700   N

Passo 9

Agora podemos usar uma das equações para determinar o valor da altura:

h = 3 P 4 b τ a d m

h = 3 ⋅ 14700   N 4 ⋅ 150   m m ⋅ 0,35   M P a

h = 210   m m

Resposta

h = 210   m m

P = 14700   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob. 55.117, quando t_0 = t_1 = t_2 = 8 m m , h_1 = 75 m m , h_2 = 60 m m e b = 50 m m .
Determinar a distribuição de tensões de cisalhamento ao longo da linha D ' B ' na perna horizontal do perfil cantoneira com o carregamento mostrado. Os eixos x ' e y ' são eixos centroidais principais
Para perfil e o carregamento do Prob. 5.130, determinar a distribuição de tensões de cisalhamento ao longo da linha D ' A ' perna vertical.
Resolver o Prob. 5.120, considerando que a espessura da placa é de 6m m e é dobrada para formar o perfil mostrado.
A viga em balanço consiste de perfil “U” de espessura uniforme. Sabendo-se que a carga P atua no centro de cisalhamento O e no plano da seção de extremidade da viga, determinar a tensão de cisalhament