Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 76
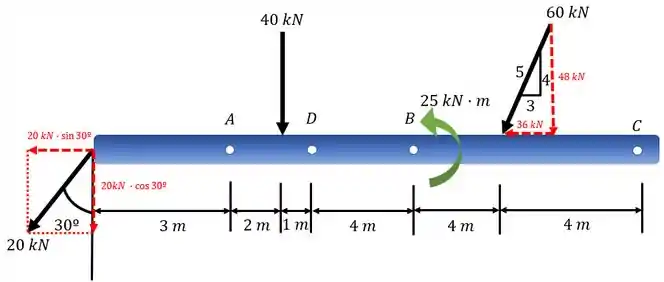
A viga composta é sustentada por pinos em C e por roletes em A e B. Existe uma dobradiça (pino) em D. Deterine as componentes da reação nos apoios. Despreze a espessura da viga.
Passo 1
Podemos começar desenhando o diagrama do corpo livre da viga:
Passo 2
As forças de e causam momento anti-horário e a força Pode-se começar aplicando a equação do equilíbrio para o momento no ponto D. Considerando o trecho do início da viga até o ponto D:
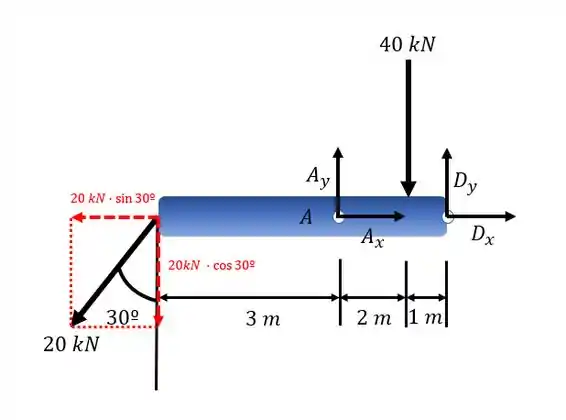
Em A temos um rolete, portanto:
Passo 3
Aplicando a equação do equilíbrio no eixo y para esse trecho:
Passo 4
Aplicando a equação do equilíbrio no eixo x:
Em D há uma dobradiça, portanto:
Passo 5
Aplicando a equação do equilíbrio para o momento no ponto C em relação ao trecho DC. As forças de , o componente Dy e o momento de causam momento no sentido anti-horário e a força causa momento no sentido horário Pode-se começar aplicando a equação do equilíbrio para o momento no ponto D. Considerando o trecho do início da viga até o ponto D:
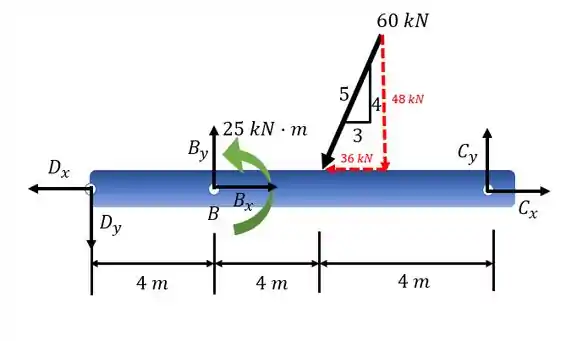
**Lembrando do princípio da ação e reação quando extraímos parte da viga para a análise. Observar o sentido de e para o trecho AD e para o trecho DC
Em B temos um rolete, portanto:
Passo 6
Aplicando a equação do equilíbrio no eixo y:
Passo 7
Aplicando a equação do equilíbrio no eixo x:
Resposta