Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 66

Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante vertical V aplicada em O.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo: começando pela inércia e vejam o esboço abaixo:

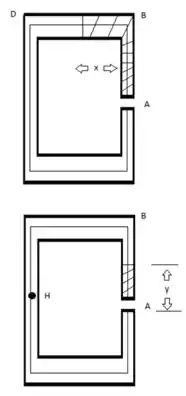
Passo 2

Determinando as inércias de cada seção temos:

I A B = 1 3 0,125 3 3 = 1,125 i n 4

I B D = 1 12 4 0,125 3 + 4 0,125 3 2 = 4,50065 i n 4

I D E = 1 12 0,125 ( 6 ) 3 = 2,25 i n 4

I E F = I B D = 4,50065 i n 4

I F G = I A B = 1,125 i n 4

I = Σ I = 13,50 i n 4  

Passo 3

(a) Parte AB:

Q y = t y y 2 = 0,5 t y ²

q y = V Q y I = 0,5 V t I y ²

F A B =   ∫ 0 3 q y d y =     0,5 V t I   ∫ 0 3 y 2 d y = 4,5 V t I ↑

Seu momento sobre H é

4 F A B = 18 V t I ↺  

Q B = 0,5 t 3 2 = 4,5 t

Passo 4

Parte BD:

Q x =   Q B + x t 3 = 4,5 , + 3 x t

q x = V q x I = V t I 4,5 + 3 x t

F B D = ∫ 0 4 q x d x = ∇ t I     ∫ 0 4 4,5 + 3 x d x =   42 V t I ←  

Seu momento sobre H:

3 F B D = 126 V t I ↺

Q D = 4,5 + 3 4 t = 16,5 t

Passo 5

Parte EF:

Por simetria com a parte BD, F E F = 42 V t I →

Seu momento sobre H é 3 F E F = 126 V t I ↺

Parte FG: Por simetria com a parte AB, F F G = 4,5 V T I ↑

Seu momento sobre H é 4 F F G = 18 V t I ↺

Momento sobre H da força na parte DE é zero.

V e = Σ M H = V t I 18 + 126 + 0 + 126 + 18 = 144 V t I

e = 144 t I = 2,88 0,125 13,50

e = 2,67   i n .

Passo 6

Para a letra (b) consideramos:

Q A = Q G = 0 τ A = τ G = 0

Q B = Q F = 4,5 t

τ B = τ F = V Q B I t = 2,75 4,5 t 13,50 t = 0,917   k s i

Q D = Q E = 16,5 t

τ D = τ E = V Q 0 I t = 2,75 16,5 t 13,50 t = 3,36   k s i

Em H (eixo neutro),

Q H = Q D + t 3 1,5 = 21 t

τ H = V Q H I t = 2,75 21 t 13,50 t τ H = 4,28   k s i

Resposta

  1. 2,67   i n
  2. 0,917   k s i , 3,36   k s i , 4,28   k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Vigas de madeira e chapas de aço são aparafusadas firmemente para formar o elemento composto mostrado na figura. Usando os dados da tabela abaixo, determine o maior momento fletor admissível quando a
Uma barra com a seção transversal mostrada na figura foi construída unindo-se firmemente latão e alumínio. Usando os dados fornecidos abaixo, determine o maior momento fletor admissível quando a barra
Para a barra composta indicada, determine o maior momento fletor admissível quando a barra é flexionada em torno do eixo vertical. Barra do problema 4.3 4 .
Vigas de madeira e chapas de aço são aparafusadas firmemente para formar o elemento composto mostrado na figura. Usando os dados da tabela abaixo, determine o maior momento fletor admissível quando a
Para a barra composta indicada, determine o raio de curvatura provocado pelo momento fletor 200N m