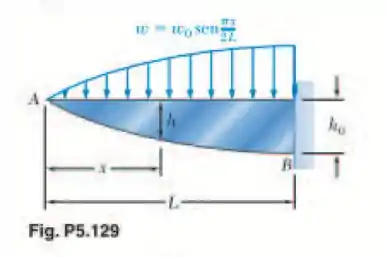
A viga AB consiste em uma placa de ferro fundido de espessura uniforme b e comprimento L e deve suportar a força w(x) mostrada. (a) Sabendo que a viga deve ser de resistência constante, expresse h em termos de x, L e . (b) Determine o menor valor de se L = 750 mm, b = 30 mm, = 300 kN/m e = 200 MPa.
Passo 1
Tá legal! Nesse exercício, não precisamos encontrar nenhuma reação de apoio para o sistema. Aqui nós vamos utilizar as equações de singularidade para encontrar o carregamento, a força cortante e o momento fletor. Então, através do carregamento do enunciado, podemos escrever o carregamento em função da distância da seguinte forma:
Agora podemos encontrar a força cortante sabendo que ela será o oposto da integral da equação do carregamento, ou seja:
Substituindo a expressão para e resolvendo a integral, chegamos em:
Agora, para encontrar o valor da constante C, nós vamos utilizar a condição de contorno que temos, que no caso é a de que não temos força cortante em , ou seja:
Então, substituindo esses valores na equação da força cortante, teremos:
Então, nossa equação para a força cortante será:
Passo 2
Agora, para encontrarmos a equação do momento fletor, como já temos a equação para a força cortante, basta lembrar que a derivada do momento equivale a força cortante, ou seja:
Isolando as variáveis dessa equação, temos:
Integrando essa expressão dos dois lados, teremos:
Agora, substituindo a expressão encontrada para no passo 1, a equação acima se torna:
Resolvendo a integral, teremos:
Em que é a constante de integração. Nesse caso, a constante de integração corresponde aos momentos localizados que são aplicados ao sistema, no nosso caso não temos nenhum momento localizado, então teremos:
Então a equação do momento será:
Passo 3
Agora, vamos utilizar a equação 5.18 vista nessa seção para escrever o módulo de resistência da viga, que será dado por:
Como você pode ver, aqui temos que colocar o módulo do momento, no entanto, a nossa equação encontrada para o momento não mostra de forma clara se será positiva ou negativa. Então vamos comparar o valor da expressão do momento em e . Começando com , temos:
Para , temos:
Podemos ver que o valor entre parênteses será negativo, pois será um valor menor que 1. Dessa forma, o módulo do momento será o valor negativo do que encontramos anteriormente, ou seja:
Substituindo a expressão para o momento na equação para o módulo de resistência, teremos:
Agora, lembrando que o módulo de resistência para uma seção transversal retangular é dado por:
Podemos igualar as duas expressões encontradas para , fazendo isso, teremos:
Agora, isolando dessa equação, chegaremos em:
Passo 4
Ainda estamos na letra (a), vamos lá! Para escrever h em termos de x, L e , está faltando determinar o , que ocorre em , então, vamos substituir esse valor de na equação que encontramos para , chegando em:
Agora precisamos dar um jeito de fazer esse termo aparecer lá na equação de . Para isso, vamos dividir a equação de por dos dois lados, dessa forma, teremos:
Tá aí! Essa é a expressão que queríamos pra .
Passo 5
Agora para resolver a letra (b), vamos utilizar a equação que encontramos para :
E vamos substituir os valores fornecidos no enunciado, chegando em um valor mínimo de :