Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 121

Para a viga constituída de um perfil laminado de aço W 5 30 × 66 e o carregamento mostrado, determinar: ( a ) a declividade na extremidade A ; ( b ) a deflexão no ponto médio C . Usar E = 200   G P a .

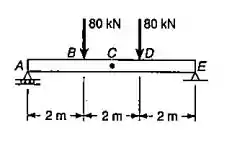
Passo 1

Fala aí galera, bora pra mais uma questão de Resmat. Neste exercício temos uma viga bi-apoiada. Por isso, através do método da superposição e utilizando fórmulas do apêndice D do nosso livro, tem-se que:

Para o primeiro carregamento:

y 1 = - P b 6 E I L L - x 3 - L 2 - b 2 L - x y 1 = - 80 × 10 3 2 36 200 × 10 9 3,51 × 10 - 6 3 3 - 32 3 y 1 = 0,43684   m

E também, temos:

y 2 = - P b 6 E I L L - x 3 - L 2 - b 2 L - x y 2 = - 80 × 10 3 4 36 200 × 10 9 3,51 × 10 - 6 3 3 - 20 3 y 2 = 0,41785   m

Com isso, temos que nossa deflexão em C é dada pela soma das duas equações da linha elástica:

y C = y 1 + y 2 y C = 0,43684   m + 0,41785   m y C = 0,85469   m

Passo 2

Em seguida, para encontrarmos a declividade no ponto A , temos que utilizar as relações de apoios fornecidas no apêndice D do livro. Além disso, :

θ A = θ A 1 + θ A 2 θ A = - P b L 2 - b 2 6 E I L - P b L 2 - b 2 6 E I L θ A = - 80 × 10 3 2 ( 6 ) 2 - 2 2 6 200 × 10 9 3,51 × 10 - 6 ( 6 ) - 80 × 10 3 4 ( 6 ) 2 - 4 2 6 200 × 10 9 3,51 × 10 - 6 ( 6 ) θ A = - 0.45584   r a d

Resposta

y C = 0,85469   m 4

- 0.45584   r a d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados, determine a reação no apoio móvel quando w 0 = 65k N / m .
Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados, sabendo que a = 2 m .w = 50 k N / m e E = 200G P a , determine (a) a inclinação no apoio em A , (b) a deflexão no ponto C .
Sabendo que a viga A E é um perfil de aço laminado 1200 x 27,4 e que P = 17,5k N ,L = 2,5m ,a = 0,8m e E = 200G P a , determine (a) a equação da linha elástica para a parte B D e (b) a deflexão o cent
Supondo que a viga A E é um perfil de aço laminado W 360 x 101 e que M 0 = 310k N m ,L = 2,4 m ,a = 0,5 m e E = 200G P a , determine (a) a equação Da linha elástica para a parte B D e (b) a deflexão n