Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 7
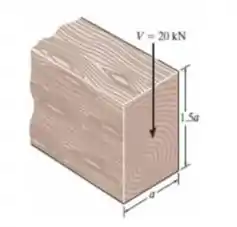
A viga tem seção transversal retangular e é feita de madeira. Se for submetida a um cisalhamento de V = 20 kN, e a = 250 mm, determine a tensão de cisalhamento máxima e trace uma curva da variação da tensão de cisalhamento na seção transversal. Faça um rascunho tridimensional do resultado.
Passo 1
Falaaaa! Ele quer a tensão de cisalhamento máxima. Como nossa seção é retangular, isso ocorre no meio da nossa seção.
Sabendo disso, vamos aplicar a fórmula de tensão de cisalhamento, beleza?
Vamos começar calculando o momento de inércia da seção transversal para :
É bom, porque é uma grandeza física que a gente vai precisar. Bora seguir!
Passo 2
E agora o momento estático do centro (onde a tensão cisalhante é máxima). Como a gente faz? Cara o momento estático é o produto entre a área acima da linha onde a gente quer calcular a tensão e .
Como a gente quer calcular a tensão no meio da seção, a nossa área é a parte da seção acima disso, ou seja, a metade da área total:
E é o a coordenada do centroide dessa área que a gente acabou de calcular. Como ela é retangular e considerando a origem dos eixos no centroide de toda a seção:
Aí o fica:
Passo 3
Por fim, a gente substitui os valores na fórmula da tensão cisalhante:
Sendo que é o nosso esforço cortante e a espessura da nossa seção na linha onde a tensão é máxima, .
Passo 4
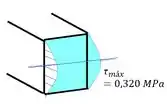
A tensão cisalhante se distribui na seção como uma parábola e tem seu máximo no centro da mesma, então:
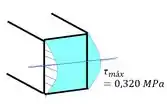
Resposta
