Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 40

A viga está sujeita a um cisalhamento V = 800   N . Determine a tensão de cisalhamento média desenvolvida nos pregos ao longo dos lados A e B se eles estiverem espaçados de s = 100 m m . Cada prego tem diâmetro de 2 m m

Passo 1

Dados da questão: V = 800   N ,   s = 100 m m ,   d p r e g o = 2 m m

A questão pede a tensão de cisalhamento sobre os pregos: τ p r e g o = ?

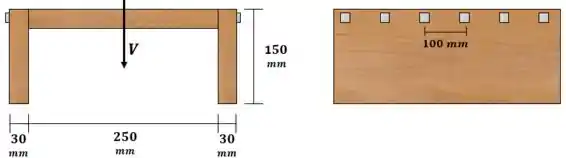
Estratégia de resolução:

Quase todas as questões de fluxo de cisalhamento começam com as suas definições geométricas: Centroide, Momento de Inércia e Momento Estático. Nesta etapa é comum ocorrer erros no cálculo do momento estático. Tenha atenção!

Depois calculamos o fluxo de cisalhamento, e com o fluxo de cisalhamento podemos calcular a força sobre cada parafuso. Finalizamos a questão calculando a tensão de cisalhamento sobre o parafuso.

Passo 2

Começamos calculando o centroide y C :

y c = ∑ A ⋅ y ∑ A

y c = A v e r d e ⋅ y v e r d e + 2 ⋅ A a z u l ⋅ y a z u l A v e r d e + 2 A a z u l

y c = 250 ⋅ 30 ⋅ 135 + 2 ⋅ 150 ⋅ 30 ⋅ 75 250 ⋅ 30 + 2 ⋅ 150 ⋅ 30

y c = 102,272   m m

Passo 3

Agora calculamos o momento de inércia de toda a seção transversal em relação ao centroide

I = I v e r d e + 2 ⋅ I a z u l

I = 250 ⋅ 30 3 12 + 250 ⋅ 30 ⋅ 32,727 2 + 2 ⋅ 30 ⋅ 150 3 12 + 30 ⋅ 150 ⋅ 27,272 2

I = 32,16 ⋅ 10 6   m m 4

Passo 4

Agora vamos escolher e calcular o momento estático.

Existem várias formas de calcular o momento estático. Por facilidade, vamos escolher a tábua central:

Q = 250 ⋅ 30 ⋅ 32,727

Q = 245452,5   m m 3

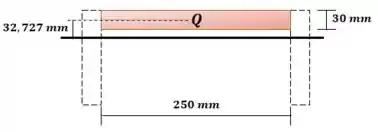
Passo 5

Veja na figura abaixo:

Observe que há um espaçamento s = 100 m m entre os parafusos, e que à medida que o fluxo de cisalhamento avança sobre a área que foi escolhida pro momento estático, ele gera um cisalhamento em dois parafusos. Essa relação é dada dessa forma:

q = 2 F p a r a f u s o s

O número dois aparece na equação acima, pois o fluxo resiste a 2 pregos simultaneamente.

Por outro lado, a fórmula para o fluxo de cisalhamento é

q = V ⋅ Q I

Igualando as duas equações:

V ⋅ Q I = 2 F p a r a f u s o s

Isolando F p a r a f u s o :

F p a r a f u s o = V Q ⋅ s 2 I

F p a r a f u s o = 800 N ⋅ 245452,5   m m 3 ⋅ 100   m m 2 ⋅ 32,16 ⋅ 10 6   m m 4

F p a r a f u s o = 305,29   N

Passo 6

Agora vamos calcular a tensão sobre o parafuso.

A p a r a f u s o = π d p a r a f u s o 2 4 = π ⋅ 2 2 4 = π   m m 2

τ = F p a r a f u s o A p a r a f u s o = 305,29 π ⋅ N m m 2

τ = 97,17   M P a

Resposta

τ = 97,17   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga suporta um cisalhamento vertical V = 35k N . Determine a força resultante desenvolvida no segmento AB.
A escora de alumínio tem 10mm de espessura e a seção transversal mostrada na figura. Se for submetida a um cisalhamento V = 150N , determine o fluxo de cisalhamento nos pontos A e B.
O tubo está sujeito a uma força de cisalhamento V = 40k N . Determine o fluxo de cisalhamento no tubo nos pontos A e B
A viga é composta por quatro chapas e está sujeita a uma força de cisalhamento V = 25k N . Determine o fluxo de cisalhamento máximo na seção transversal.
A escora de alumínio tem 10 m m de espessura e a seção transversal mostrada na figura. Se for submetida a um cisalhamento V = 150N , determine o fluxo de cisalhamento máximo na escora.