Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 21
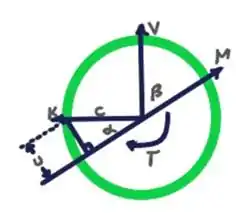
Foi definido na Seção 8,2 que as tensões de cisalhamento produzidas em um eixo pelas cargas transversais são geralmente muito menores que aquela produzidas por torque . Nos Problema anteriores, seu efeito foi ignorado, e considerou-se que a tensão de cisalhamento máxima determinada seção ocorrida em pouco um ponto H(Fig.P8.21a)e era igual à expressão obtida na Equação (8,5). ou seja .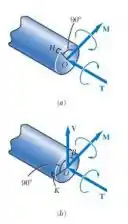
Mostre que a tensão de cisalhamento máxima no ponto K(Fig. P8.21a), em que o efeito da força cortante V é maior, pode ser expressa como
em que é o ângulo entre os vetores V e M.Está claro que o efeito da força cortante V não pode ser ignorado quanto (Dica:Somente a componente M ao longo de V contribui para a tensão de cisalhamento em K.)
Passo 1
Então turminha, parece ser complicado este cálculo,mas veremos que não é bem assim! Vamos calcular?
Tensão de cisalhamento no ponto K:
Devido a V:
Para um semi círculo:
Para um corte circular em seu diâmetro:
Para uma seção circular:
Passo 2
Devido a T:
Uma vez que as tensões de cisalhamento tem a mesma orientação, teremos:
Tensão de flexão no ponto K:
Passo 3
Onde é a distância entre o ponto K e o eixo neutro:
Usando o círculo de Mohr:
Corte transversal é dado por:
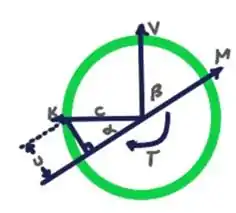
Resposta
