Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 109
Um torque de é aplicada à extremidade de um tanque contendo óleo sob uma pressão de . Sabendo-se que o tanque tem um diâmetro externo de e uma espessura de , determinar a máxima tensão normal e a máxima tensão de cisalhamento na parede cilíndrica do tanque.
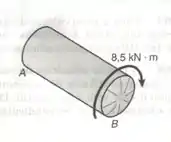
Passo 1
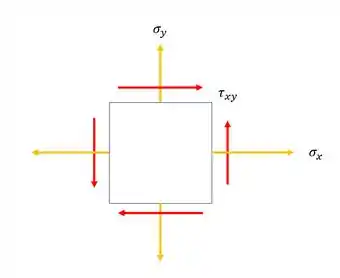
Então galera, essa questão pode parecer que foge da nossa realidade, mas muito pelo contrário, ela só vai acoplar um conceito novo ao nosso problema, e esse conceito é muito simples. Você lembra como era o nosso elemento infinitesimal quando o mesmo estava sujeito a um conjunto de tensões?
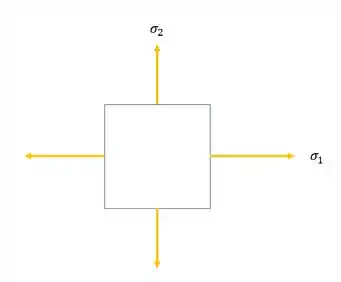
Porém, sempre que tratamos vasos de pressão, ou esferas de pressão, calculávamos um estado de tensões sem tensão de cisalhamento, ou seja, só tensões principais, que é exatamente isso aqui que calculamos:
Agora pensa comigo, sempre que colocamos uma torção em uma estrutura, qual o tipo de tensão que ela gera???? Isso mesmo, a tensão cisalhante, ou seja, a nossa fórmula é dada por:
Em que o J é dado por:
E quando tivermos essa tensão cisalhante agindo na nossa seção, o nosso elemento será dado por:
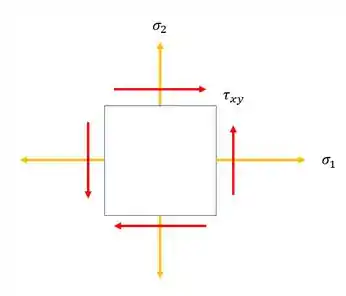
Onde as tensões normais são calculadas da seguinte maneira.
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na nossa estrutura
Até aqui tudo certo, certo? Mas ai entra uma coisa bem legal, lembra que o enunciado quer saber as TENSÕES máximas cisalhante e normal, e agora que temos um elemento infinitesimal, como vamos fazer para determinar as tensões máximas? Só lembrar das nossas fórmulas dadas por:
Sabemos que:
Agora sim temos toda a matéria prima para resolver o nosso problema, vamos nessa??
Passo 2
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
E agora só falta a tensão cisalhante, que vai vir da torção, e para isso temos as seguintes equações:
Em que o J é dado por:
E assim o nosso elemento infinitesimal é dado por:
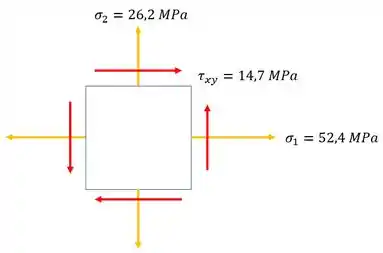
Passo 3
E agora que temos o elemento infinitesimal, precisamos apenas das tensões principais, e essas tensões principais são dadas pela seguinte equação.
E assim já temos a tensão máxima cisalhante agindo no nosso elemento infinitesimal.
As tensões principais normais são dadas por: