Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 25

A viga caixão tem tensão de flexão admissível σ a d m = 10   M P a e tensão de cisalhamento admissível τ a d m = 775   M P a . Determine a intensidade máxima w da carga distribuída que ela pode suportar com segurança. Calcule também o espaçamento máximo seguro entre os pregos para cada terço do comprimento da viga. Cada prego pode resistir a uma força de cisalhamento de 200 N.

Passo 1

Dados da questão: L = 6 m ,   τ a d m = 775   M P a ,   σ a d m = 10   M P a ,   H = 250   m m ,   B = 210   m m ,   t = 30   m m ,   h = 190   m m ,     b = 150   m m ,   F p r e g o = 200   N .

A questão pede: w = ? ,   s =   ?

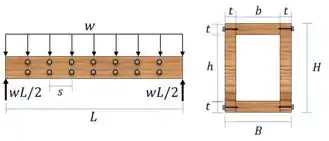
Passo 2

Vamos começar calculando as reações de apoio

∑ M B = 0 ⇒ R A ⋅ L - w L ⋅ L 2 = 0

R A = w L 2

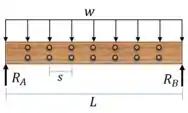
Por simetria:

R A = R B = w L 2

Passo 3

Vamos utilizar o método das seções para gerar as equações de força cortante e momento fletor.

∑ F Y = 0 ⇒ w L 2 - w x - V x = 0

V x = w L 2 - w x

∑ M B = 0 ⇒ - w L 2 ⋅ x + w x ⋅ x 2 + M ( x ) = 0

M x = w L 2 x - w x 2 2

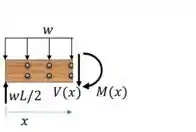
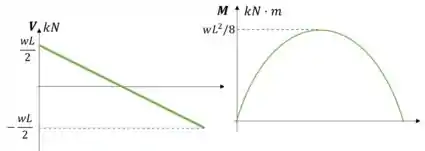
Os máximos são:

M m a x = w L 2 8

V m a x = w L 2

Passo 4

Vamos calcular o momento de inércia:

I = B ⋅ H 3 12 - b h 3 12

I = 210 ⋅ 250 3 12 - 150 ⋅ 190 3 12

I = 187,7 ⋅ 10 6   m m 4  

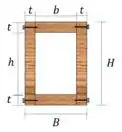
Passo 5

Para testar a resistência da viga sobre cisalhamento, precisamos calcular o momento estático máximo:

Q m a x = b ⋅ t ⋅ h 2 + t 2 + 2 ⋅ H 2 ⋅ t ⋅ H 4

Q m a x = 150 ⋅ 30 ⋅ 190 + 30 2 + 2 ⋅ 250 2 ⋅ 30 ⋅ 250 4

Q m a x = 963750   m m 3

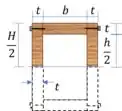
Passo 6

Para calcular o espaçamento dos parafusos vamos calcular o momento estático de uma das tábuas:

Q p r e g o = 2 ⋅ H 2 ⋅ t ⋅ H 4

Q p r e g o = 2 ⋅ 250 2 ⋅ 30 ⋅ 250 4

Q p r e g o = 468750   m m 3

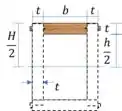
Passo 7

Agora vamos calcular o carregamento w de acordo com a resistência à flexão:

σ a d m = M m a x ⋅ c I

σ a d m = w L 2 8 ⋅ H 2 I

Isolando o w :

w = σ a d m ⋅ I ⋅ 2 H ⋅ 8 L 2

Aplicando os valores:

w = 10   M P a ⋅ 187,7 ⋅ 10 6   m m 4 ⋅ 2 250   m m ⋅ 8 ( 6000   m m ) 2

w = 3,34   N ⋅ m m

w = 3,34   k N ⋅ m

Passo 8

Vamos calcular o carregamento w de acordo com a resistência ao cisalhamento:

τ a d m = V m a x Q m a x I ⋅ 2 t

τ a d m = w L 2 ⋅ Q m a x I ⋅ 2 t

Isolando w :

w = 4 τ a d m I t Q m a x L

w = 4 ⋅ 775   M P a ⋅ 187,7 ⋅ 10 6   m m 4 ⋅ 30   m m 963750   m m 3 ⋅ 6   m

w = 3018   N ⋅ m m

w = 3018   k N ⋅ m

Passo 9

Para garantir a resistência, selecionamos o menor dos carregamentos

w = 3,34   k N ⋅ m

Passo 10

  • Utilizando o carregamento w calculado, para o primeiro teço da viga. Neste primeiro teço o maior cisalhamento é o cisalhamento máximo:

    • 2 F p r e g o s 1 = V m a x Q p r e g o I

    s 1 = 2 F p r e g o I V m a x Q p r e g o

    s 1 = 2 F p r e g o I w L 2 Q p r e g o

    s 1 = 4 F p r e g o I w L Q p r e g o

    s 1 = 4 ⋅ 200   N ⋅ 187,7 ⋅ 10 6   m m 4 3,34   k N ⋅ m ⋅ 6   m ⋅ 468750   m m 3

    s 1 = 15,98   m m

  • Para o segundo terço da viga o maior cisalhamento está no ponto x = L 3

    • V L 3 = w L 2 - w L 3 ⇒ V 2 = w L 6

    E o espaçamento será:

    s 2 = 2 F p r e g o I V 2 Q p r e g o

    s 2 = 12 F p r e g o I w L Q p r e g o

    s 2 = 12 ⋅ 200   N ⋅ 187,7 ⋅ 10 6   m m 4 3,34   k N ⋅ m ⋅ 6   m ⋅ 468750   m m 3

    s 2 = 47,94   m m

  • Para o terço final da viga o cisalhamento é:

V 3 = - V m a x

Como a intensidade do cisalhamento é igual a intensidade do primeiro terço, podemos garantir que

s 3 = s 1 = 15,98   m m

Resposta

w = 3,34   k N ⋅ m

s 3 = s 1 = 15,98   m m

s 2 = 47,94   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensã
Determinar a tensão cisalhamento no ponto A de um tubo na parede fina como a seção transversal mostrada, casada por uma força cortante vertical V.
O projeto de uma viga requer a soldagem de quatro placas horizontais à uma placa vertical de 12,7x127 mm como mostrado. Para uma força cortante vertical V determinar a dimensão h para que o fluxo de c
Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi
Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi