Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 17
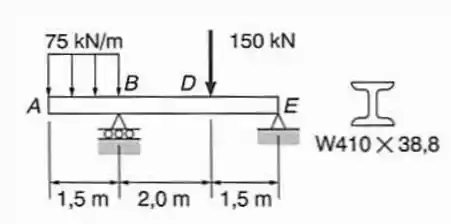
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos e : (a) a maior tensão normal; (b) a maior tensão de cisalhamento, usando a aproximação sugerida na Sec. 5.6.
Passo 1
Para achar a maior tensão normal vamos fazer o seguinte:
- Calcular o momento fletor da barra.
- Calcular onde a linha neutra se encontra.
- Calcular o momento de inércia da barra.
- Substituir na equação da tensão.
E para achar a maior tensão de cisalhamento:
- Calcular a força cortante da barra.
- Substituir na equação da tensão.
Passo 2
Vamos calcular o momento fletor e aforça cortante na barra. Para isso vamos aplicar logo o momento em relação ao ponto , lembrando que vamos considerar a carga distribuída como uma carga pontual atuante no seu centro.
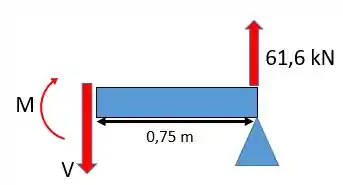
Como só existem duas forças podemos ver que a força cisalhante é igual à reação em E:
Agora, calculando o momento fletor:
Passo 3
Cálculo da linha neutra:
Aí, gente, se liga no macete monstro! A área da seção transversal é simétrica então nem precisa calcular a linha neutra, ela vai estar exatamente no meio da figura!
Esse valor veio da tabela dos perfis de abas retas
Passo 4
O momento de inércia também é fornecido pela tabela:
Passo 5
Agora vamos substituir na equação da tensão:
A maior tensão normal ocorrerá no ponto mais distante do centroide, logo em .
Passo 6
Utilizando a propriedade fornecida:
Pela tabela:
Resposta
a)
b)