Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 151

Para a viga indicada, determinar a tensão no ponto A , considerando que o plano no qual atua o momento M foi girado de 90 ° no sentido horário.

Passo 1

Para resoluções de questões deste tipo temos de desenhar o ciclo de Mohr, para determinar os eixos principais e os correspondentes momentos de inércia. Depois vamos Decompor o momento M na direção destes eixos e finalmente calcular a tensão. Ou seja, vamos seguir o seguinte passo-a-passo:

  1. Desenhar o ciclo de Mohr.
  2. Achar os eixos principais.
  3. Decompor o momento sobre estes eixos.
  4. Achar os pontos u e v relativos ao novo eixo.
  5. Calcular a tensão com relação aos novos eixos.

A diferença agora é que o momento M não está mais em z , como foi rotacionado de 90 ° no sentido horário, agora está em y

Passo 2

Desenhar o ciclo de Mohr, nós temos a forma geral:

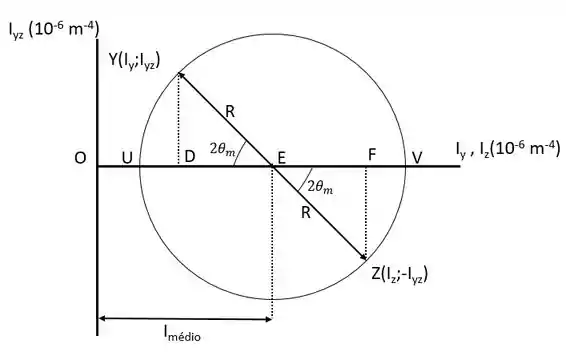
Os momentos do inércia já foram dados então precisamos calcular o ângulo 2 θ m da seguinte forma:

t g ( 2 θ m ) = F Z E F

E calculamos também o raio R da forma:

R 2 = E F 2 + ( F Z ) ²

Assim como o I m é d i o

I m é d i o = I y + I z 2

Show de bola! Agora é só substituir os valores que a gente tem na nossa questão:

I m é d i o = 7,24 + 2,61 2 = 4,925

Calculando o ângulo 2 θ m

t g ( 2 θ m ) = F Z E F

t g ( 2 θ m ) = 2,54 4,925 - 2,61

t g ( 2 θ m ) = 2,54 2,315

t g ( 2 θ m ) = 1,0972

2 θ m = 47,65 °

Logo

θ m = 47,65 ° 2 = 23,83 °

Achando o raio R :

R 2 = 2,315 2 + ( 2,54 ) ²

R 2 = 11,811

R = 11,811 = 3,437 × 10 - 6   m 4

Passo 3

Agora vamos achar os eixos principais, essa parte é mais tranquila do que a anterior e consiste basicamente em achar os pontos U e V :

I u = I m é d i o + R

I u = 4,925 + 3,437 = 8,362 × 10 - 6   m 4

I v = I m é d i o - R

I u = 4,925 - 3,437 = 1,488 × 10 - 6   m 4

Podemos observar que:

I m á x = I u = 8,362 × 10 - 6   m 4

I m í n = I v = 1,488 × 10 - 6   m 4

Passo 4

Agora vamos decompor o momento M sobre estes eixos ( U e V ) que acabamos de encontar. Note que o novo eixo ficará da seguinte forma.

M u = M ⋅ c o s ( θ m )

M u = 3 ⋅ c o s 23,83 ° = 2,744   k N ⋅ m

M v = - M ⋅ s e n ( θ m )

M v = - 3 ⋅ s e n 23,83 ° = - 1,212   k N ⋅ m

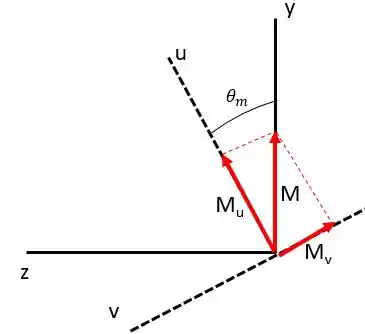
Passo 5

Já os novos pontos nós vamos achar de forma parecida, como mostrado, de forma genérica, abaixo:

u A = y A ⋅ c o s ( θ m ) + z A ⋅ s e n ( θ m )

u A = ( - 102 + 25,1 ) ⋅ c o s ( 23,83 ° ) + 50,5 ⋅ s e n ( 23,83 ° )

u A = - 70,34 + 20,40 = - 49,94   m m

v A = - y A ⋅ s e n ( θ m ) + z A ⋅ c o s ( θ m )

v A = - ( - 102 + 25,1 ) ⋅ s e n ( 23,83 ° ) + 50,5 ⋅ c o s ( 23,83 ° )

v A = 31,07 + 46,19 = 77,26   m m

Passo 6

Calcular a tensão relativa aos eixos u e v

σ A = M u ⋅ v A I u - M v ⋅ u A I v

σ A = 2 744     ⋅ 0,07726 8,362 × 10 - 6 - - 1 212 ⋅ - 0,04994 1,488 × 10 - 6

σ A = 25,35 - 40,68 = - 15,33   M P a

Resposta

σ A = - 15,33   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qualquer dar três cargas axiais, de intensidade P = 45 kN podem ser aplicadas na extremidade de um perfil de aço laminado w200 × 31,3. Determinar a tensão no ponto A: (a) para o carregamento mostrado;
Resolva o Prob. 4,114, considerando que a barra é substituída por um tupo de 20 mm de diâmetro externo e 16 mm de diâmetro interno.
Sabendo-se que a tensão admissível na seção ABD é 70 MPa, determinar a maior força P que pode ser aplicada ao suporte mostrado.
Um desvio h deve ser executado em uma barra circular maciça. Sabendo-se que a máxima tensão, depois desse desvio ser executado, não deve exceder três vezes a tensão na barra quando era reta, determina
Resolva o problema 4.112, assumindo que a carga de 20 kN é removida.