Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 26

A viga foi construída com três tábuas como mostra a figura. Se cada prego puder suportar uma força de cisalhamento de 250   N , determine o espaçamento máximo entre os pregos s, s’, s’’, para as regiões AB, BC, CD, respectivamente.

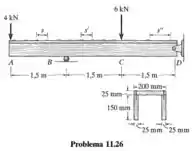
Passo 1

Dados da questão: F p r e g o = 250   N ,   t = 25   m m ,   h = 150 m m ,   H = 175 m m ,   B = 200   m m ,   b = 150   m m .

Vamos começar com as reações de apoio.

∑ M D = 0 ⇒ 4 ⋅ 3 L - R B ⋅ 2 L + 6 ⋅ L = 0

R B = 9   k N

∑ F Y = 0 ⇒ - 4 + R B - 6 + R D = 0

R D = 1   k N

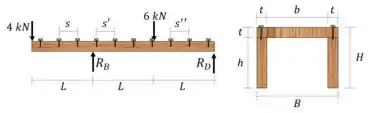
Passo 2

Utilizamos a tabela 6.1 para gerar os diagramas de esforço cortante pelo método gráfico.

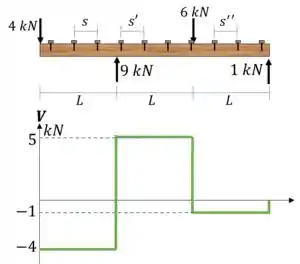
Passo 3

Para determinar o espaçamento, vamos precisar antes calcular o momento de inércia e o momento estático.

y c = t ⋅ B ⋅ h + t 2 + 2 ⋅ h ⋅ t ⋅ h 2 t ⋅ B + 2 ⋅ h ⋅ t

y c = 25   m m ⋅ 200   m m ⋅ 162,5   m m + 2 ⋅ 150   m m ⋅ 25   m m ⋅ 150 2 25   m m ⋅ 200   m m + 2 ⋅ 150   m m ⋅ 25   m m

y c = 110   m m

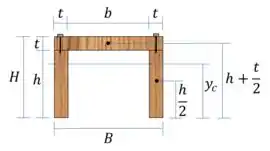
Passo 4

Vamos calcular o momento de inércia da seção.

I = B ⋅ t 3 12 + B ⋅ t ⋅ h + t 2 - y c 2 + 2 t ⋅ h 3 12 + t ⋅ h ⋅ y c - h 2 2

I = 200 ⋅ 25 3 12 + 200 ⋅ 25 ⋅ 52,5 2 + 2 25 ⋅ 150 3 12 + 25 ⋅ 150 ⋅ 35 2

I = 37,29 ⋅ 10 6   m m 4

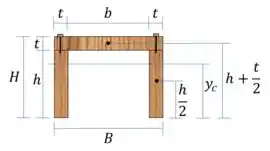
Passo 5

Q p r e g o = t ⋅ B ⋅ h + t 2 - y c

Q p r e g o = 25 ⋅ 200 ⋅ 52,5

Q p r e g o = 262500   m m 3

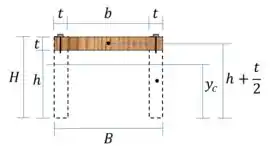
Passo 6

Vamos analisar o esforço sobre os pregos no primeiro terço da viga. Nesta região o esforço cortante é:

V 1 = - 4   k N

Agora vamos analisar o esforço sobre os pregos:

2 F p r e g o s s = V 1 Q p r e g o I

s = 2 F p r e g o s I V 1 Q p r e g o

s = 2 ⋅ 250   N ⋅ 37,29 ⋅ 10 6   m m 4 4 k N ⋅ 262500   m m 3

s = 17,76   m m

Passo 7

Vamos analisar o esforço sobre os pregos na parte central da viga. Nesta região o esforço cortante é:

V 2 = 5   k N

Agora vamos analisar o esforço sobre os pregos:

2 F p r e g o s s ' = V 2 Q p r e g o I

s ' = 2 F p r e g o s I V 2 Q p r e g o

s ' = 2 ⋅ 250   N ⋅ 37,29 ⋅ 10 6   m m 4 5   k N ⋅ 262500   m m 3

s ' = 14,21   m m

Passo 8

E terminamos analisando o último terço da viga.

V 3 = - 1   k N

Agora vamos analisar o esforço sobre os pregos:

2 F p r e g o s s ' ' = V 3 Q p r e g o I

s ' ' = 2 F p r e g o s I V 3 Q p r e g o

s ' ' = 2 ⋅ 250   N ⋅ 37,29 ⋅ 10 6   m m 4 1   k N ⋅ 262500   m m 3

s ' ' = 71,03   m m

Resposta

s = 17,76   m m

s ' = 14,21   m m

s ' ' = 71,03   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensã
A seção transversal de uma viga extrudada é uma seção quadrada vazada de lado a = 75m m e espessura t = 6,35m m . Para uma força cortante vertical 65k N , determinar a máxima tensão de cisalhamento na
Para uma viga feita de dois ou mais materiais com diferentes módulos de elasticidade, mostra que a Eq. 510 τ = V Q I t Permanece válida, desde que os valores de Q e I sejam calculados usando a seção t
Uma viga composta é feita de madeira e duas chapas de aço, unidas com parafusos, como mostrado. Sabendo-se que os parafusos são de 16m m de diâmetro e espaçados longitudinalmente de 200m m , os módulo
Uma barra de aço ( E a = 200G P a ) e uma de alumínio ( E a l = 70G P a ) são firmemente unidas para formar a viga composta mostrada. Para uma força cortante vertical de 20k N , determinar (a) a tensã