Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 126

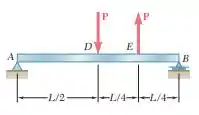
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a deflexão no ponto D   e (b) a inclinação na extremidade A .  

Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

O primeiro passo é aplicar as equações de somatório de momento nos dois apoios. Com isso, teremos:

∑ M B = 0

- R A L + P L 2 - P L 4 = 0

R A = 1 4 P

∑ M A = 0

- P L 2 + P 3 L 4 + R B L = 0

R B = - 1 4 P

Passo 2

Agora, vamos desenhar o gráfico de M E I :

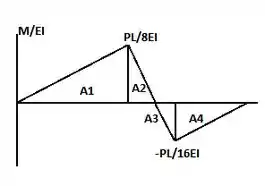
Calculando as áreas:

A 1 = 1 2 1 8 P L E I L 2 = 1 32 P L 2 E I

A 2 = 1 2 1 8 P L E I L 6 = 1 96 P L 2 E I

A 3 = 1 2 - 1 16 P L E I L 12 = - 1 384 P L 2 E I

A A = 1 2 - 1 16 P L E I L 4 = - 1 128 P L 3 E I

Agora, vamos calcular a tangente de referência, que será a área do gráfico acima vezes a distância do ponto ao centroide da área. Neste caso, cada área multiplicada pela distância de seu centroide ao ponto.

Como as contas aqui são grandes, vou colocar só o resultado.

t B A = 3 128 P L 3 E I

t D A = 1 32 P L 2 E I 1 3 L 2 = 1 192 P L 3 E I

Passo 3

Com os dados calculados, podemos determinar o que foi pedido. A deflexão em D será:

y D = t D A - x D L t B A

y D = - 5 768 P L 3 E I

Passo 4

Da mesma forma, a inclinação em A   será:

θ A = - t B A L = - 3 128 P L 2 E I

Prontinho, questão finalizada!

Resposta

  1. y D = - 5 768 P L 3 E I
  2. θ A = - 3 128 P L 2 E I
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a inclinação e a deflexão em B. EI é constante.
Se os mancais exercem somente reações verticais sobre o eixo, determine a inclinação nos mancais e a deflexão máxima do eixo. EI é constante.
Para a viga de madeira e o carregamento mostrados na figura, determine (a) a inclinação no ponto A e (b) a deflexão no ponto C. Use E = 11,72 GPa.
Para a viga e o carregamento mostrados na figura, determine (a) a inclinação no ponto A e (b) a deflexão no ponto D. Use E = 200 GPa.
Para a viga e o carregamento mostrados na figura, determine (a) a inclinação no ponto A e (b) a deflexão no ponto A.