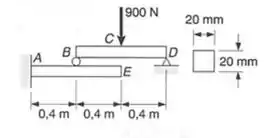
A viga BD repousa sobre a viga em balanço AE, como mostrado. Sabendo-se que uma barra quadrada de lado é usado para cada uma das vigas, determinar a deflexão, para o carregamento indicado, no:

1. Ponto E . Usar

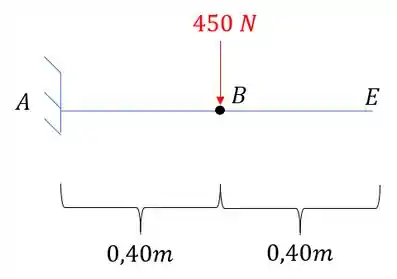
Olhando a nossa viga ABE, temos a seguinte viga obtida no item A, exatamente com o carregamento que já obtemos, assim, temos que:

Assim a tabela que podemos usar, é a seguinte:

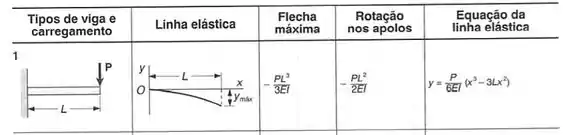
Precisamos ver que não temos a equação exata para o ponto E, mas podemos usar a nossa equação exatamente até o ponto B e depois, a partir do ponto B, podemos chegar no ponto E, assim, temos que:

Sabemos que:

E a inércia no fim da tabela é dada por:

Assim a deformação em b é dada por:

E olhando o ângulo em B, teremos que:

E a deformação em E, considerando a distância entre B e E como , teremos que:

Assim tem-se que: