Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 129
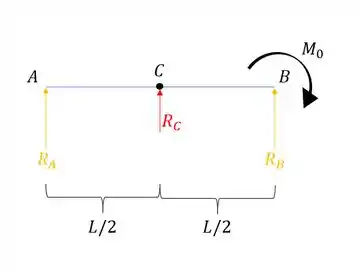
Para a viga uniforme mostrada, determinar a reação em cada um dos três apoios.
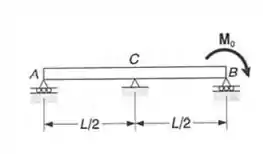
Passo 1
Então galerinha, nesse problema temos que tomar cuidado porque se trata de uma viga estaticamente indeterminada, e aqui vamos usar um conceito novo. Basta fazermos o seguinte, vamos transformar a nossa viga em uma viga estática, e no lugar do apoio, vamos por uma carga, que é a nossa reação, e vai ser aí que a nossa magica vai acontecer.
Com isso, vamos acabar com o apoio em C e transformar ele em uma carga, assim, vamos ter que:
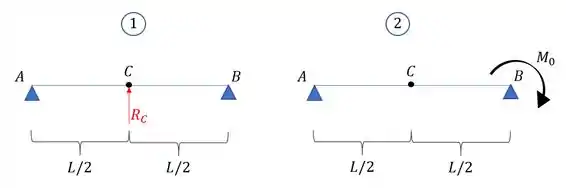
Agora olha a mágica, perceba que dividi a viga em 2 , certo? E porque fiz isso? Porque pensa só, eu sei que onde tem é um apoio, certo? Logo, quando é a deformação lá? Zero, certo? Agora pensa comigo, se eu calcular a deformação em C pra viga 1 ali em cima, e somar com a deformação em C na viga 2, quanto tem que ser a deformação total? ZEEERO, certo? Então vamos fazer isso.
Passo 2
- Deformação no ponto C na viga 1
- Deformação no ponto C na viga 2
Sabemos que a tabela no fim do livro é dada por:
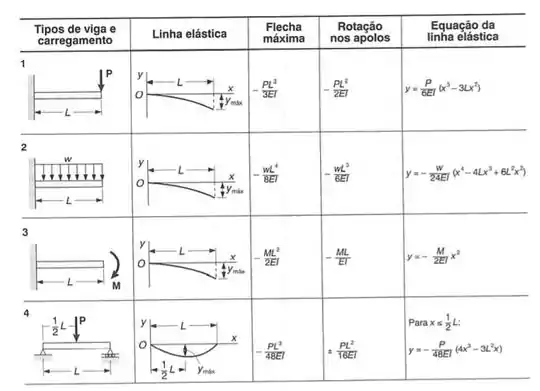
Por essa tabela vemos que a deformação no ponto C da viga para uma carga concentrada é dada por (e lembra como a carga é de baixo pra cima, vamos trocar o sinal da fórmula, assim, vamos ter que)
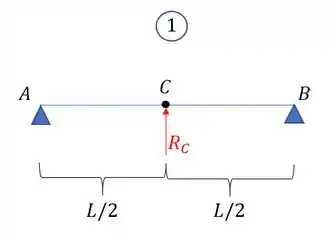
Pela tabela temos que a máxima deformação que ocorre no ponto C onde tem a deformação é dada por (lembrar que como a carga é de baixo pra cima, vai gerar uma deformação positiva):
Sabemos que a tabela no fim do livro é dada por:
Por essa tabela vemos que a deformação no ponto C da viga para uma carga concentrada é dada por (e lembra como a carga é de baixo pra cima, vamos trocar o sinal da fórmula, assim, vamos ter que)
Usando a nossa equação para o ponto C com , assim, temos que:
E agora temos apenas as duas deformações, podemos continuar a nossa conta:
Passo 3
O que concluímos? Se somarmos as deformações em A eles tem que ser zero, certo? Já que é um apoio, assim, podemos fazer o seguinte:
E assim determinamos a reação em C, assim, vamos calcular as outras reações.
Passo 4
Sabemos que as nossas vigas e as reações que precisamos é dada por:
Sabemos que o somatório de momentos em B é dado por:
Substituindo temos que:
E para o somatório de forças verticais, temos que:
