Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 27

Uma viga com a seção transversal mostrada é submetida a uma força cortante vertical V . Determine (a) a linha horizontal ao longo da qual a tensão de cisalhamento máxima. (b) a constante k na expressão a seguir para a tensão de cisalhamento máxima.

τ m a x = k V A

em que A é a área da seção transversal da viga

Passo 1

Galerinha, vamos resolver este problema rapidinho, me acompanhem! O enunciado pede que a gente encontre a linha horizontal ao longo da qual a tensão de cisalhamento máxima e a constante k na expressão a seguir para a tensão de cisalhamento máxima. Para isso considere o esboço abaixo ;)

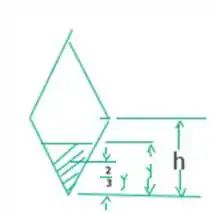
Considere as equações da área e da inercia respectivamente :D

A = 2 1 2 b h = b h I = 2 1 12 b h 3 = 1 6 b h 3

Para um corte na localização y, onde, y ≤ h ,

A y = 1 2 b y h y = b y 2 3 l t

y y = h - 2 3 y

y Q y = A y = b y 2 2 - b y 3 3 h

t y = b y h

τ y = V Q I t = V 6 b h 3 ⋅ h b y ⋅ b y 2 2 ⋅ b y 3 3 h = V b h 3 y h - 2 y h 2

Passo 2

(a)Para encontrar a localização de no máximo r , conjunto

d t d y = 0

d t d y = V b h 2 3 - 4 y m h = 0

y m h = 3 4 , i . e , ± 1 4 (Linha neutra)

Passo 3

A constante k na expressão a seguir para a tensão de cisalhamento máxima

(b) τ y m = V b h 3 3 4 - 2 3 4 2 = 9 V 8   b h = 1,125 V A

k = 1,125

Resposta

(a) y m h = 3 4 , i . e , ± 1 4 h

(b) k = 1,125 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo está apoiado sobre mancais que não oferecem resistência a carga axial. Se a tensão normal admissível para o eixo for σ a d m = 80M P a , determine, com aproximação de 1m m , o menor diâmetro do
O eixo é suportado por mancais em A e B que exercem sobre o eixo somente as componentes da força nas direções x e z. Se a tensão normal admissível para o eixo for σadm = 105 MPa, determine, com aproxi
O eixo está apoiado sobre mancais que não oferecem resistência a carga axial. Se a tensão de cisalhamento admissível para o eixo for τ a d m = 35M P a , determine, com aproximação de 1m m , o menor di
O eixo é suportado por mancais em A e B que exercem sobre o eixo somente as componentes da força nas direções x e z . Se a tensão normal admissível para o eixo for σ a d m = 105M P a , determine, com
A polia acoplada à extremidade do eixo está sujeita à carga mostrada na figura. Se os mancais em A e B exercerem somente as componentes y e z da força sobre o eixo, determine o torque de equilíbrio T