Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 5

A viga simplesmente apoiada é feita de madeira com tensão de flexão admissível σ a d m = 7   M P a e a tensão de cisalhamento admissível τ a d m = 0,5   M P a . Determine as dimensões da viga se ela tiver de ser retangular e apresentar relação altura/largura de 1,25.

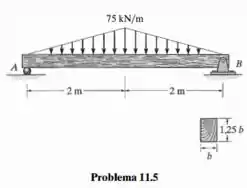
Passo 1

Reações de apoio:

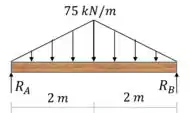
Por simetria:

R A = R B

∑ F y = 0 ⇒ R A + 75 ⋅ 4 2 + R B = 0

R A = R B = 75   k N

Passo 2

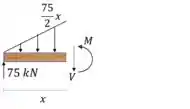
Quando 0 < x < 2   m

∑ F y = 0 ⇒ 75 - 75 x 2 ⋅ x - V = 0

V = - 75 x 2 2 + 1

∑ M = 0 ⇒ 75 x - 75 x 2 ⋅ x ⋅ x 3 - M = 0

M = 75 x - x 3 6

E geramos o gráfico. Perceba que o carregamento é simétrico, então podemos gerar um gráfico entre 0 < x < 2   m , e depois espelhar para completar o gráfico

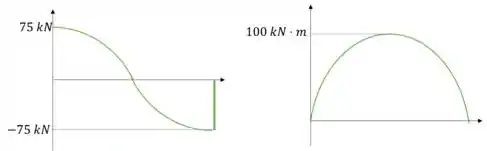
Encontramos o momento e a cortante máximos:

V = 75   k N

M = 100   k N ⋅ m

Passo 3

Aplicando a equação do momento fletor:

σ m a x = M m a x S

S = M m a x σ m a x

Lembrando que S = I / c

I c = M m a x σ m a x

1 12 b ⋅ 1,25 b 3 1,25 b / 2 = M m a x σ m a x

0,26 b 3 = M m a x σ m a x

Isolando b :

b 3 = M m a x 0,26 σ m a x

Aplicando os valores:

b 3 = 100   k N m 0,26 ⋅ 7   M P a

b = 380,1   m m

Passo 4

Vamos analisar a tensão de cisalhamento. Como a viga é retangular maciça a fórmula é

τ = 1,5   V A

Substituindo os valores:

τ = 1,5   V b ⋅ 1,25 b

τ = 1,5   V 1,25 b 2

Isolando b

b 2 = 1,5   V τ ⋅ 1,25

Aplicando os valore

b 2 = 1,5 ⋅ 75   k N 0,5   M P a ⋅ 1,25

b = 424,26   m m

Passo 5

Para garantir a resistência, escolhemos a maior dimensão:

b = 424,26   m m

Resposta

b = 424,26   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
A viga mostrada na figura suporta uma força concentrada P e seu centro. Se for feita de uma chapa com largura constante b , determine a tensão de flexão máxima absoluta na viga
A viga com avanço foi construída com duas peças de madeira de 50 mm por 100 mm escoradas como mostra a figura. Se a tensão de flexão admissível for σ a d m = 4,2M P a , determine a maior carga P que p
Determine a variação do raio r da viga em balanço que suporta a carga distribuída uniforme, de modo que ela tenha uma tensão de flexão máxima constante σ m á x á em todo o seu comprimento.