Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 23
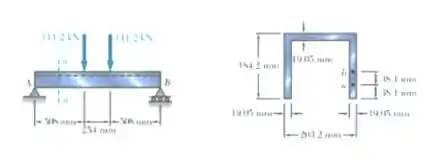
Para a viga e o carregamento mostrado, determinar a maior tensão de cisalhamento na seção n-n.
Passo 1
Falaaa.. belezinha??
Nessa questão vamos lembrar a área do retângulo:
Pra calcular o centroide:
O momento de inércia pra retângulos:
A tensão:
Passo 2
Vamos já começar dividindo a seção transversal da vida em duas partes:
E determinando algumas coisas pras duas partes:
Para a área:
- parte 1:
- parte 2: (lembrando que são duas partes iguais)
Para a posição do centro de massa:
- parte 1:
- parte 2:
E já começamos a montar nossa tabelinha...
Passo 3
Daí a gente consegue calcular o centroide:
- distância do centroide até o centro de massa da parte:
- parte 1:
- parte 2:
- momento de inércia de cada parte:
- parte 1:
- parte 2:
E finalizamos a tabelinha:
Calculando o momento de inércia geralzão:
Como a maior tensão de cisalhamento vai ser na seção transversal toda até o centroide:
Passo 4
Showw... Agora é só calcular a tensão:
Uaii... mas falta o ... Afff...
Como a figura é simétrica (), então, fazendo o somatório de forças em e igualando a zero:
E fazendo um diagrama de esforço cortante bem rapidinho (porque as forças são meio que simples, né)
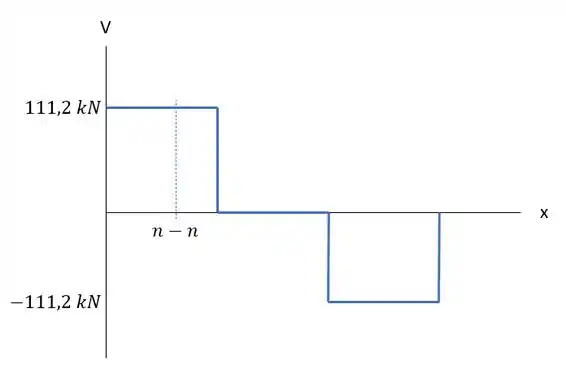
Então o na parte é .
Agora sim é só ser feliz e achar essa bendita tensão de cisalhamento máxima:
Ufa... deu trabalho essa, heim.
Mas bora pra próxima sem desanimar??