Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 92

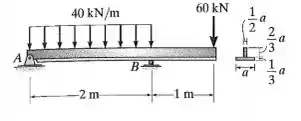
A viga está sujeita ao carregamento mostrado na figura. Se a dimensão de sua seção transversal a = 180 mm, determine a tensão de flexão máxima absoluta na viga.

Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Ele pediu a tensão de flexão máxima absoluta nesse cara. Então a gente precisa achar nele o momento máximo e usar a fórmulinha da flexão para a tensão. Bora!

Primeiramente, a gente vai começar observando as propriedades geométricas dessa seção.

Vamos determinar o momento de inércia e o centróide da seção da viga:

y c g = ∑ A y c g ∑ A = a 3 × a a 6 + 2 a 3 × a 2 2 a 3 a 3 × a + 2 a 3 × a 2 = 5 a 12 = 5 × 180 12 = 75 m m

I = ∑ b h 3 12 + A d 2

I = a 12 a 3 3 + a × a 3 5 a 12 - a 6 2 + a 24 2 a 3 3 + a 2 × 2 a 3 2 a 3 - 5 a 12 2 = 37 a 4 648

I = 59940000   m m 4

É isso. Vamos seguir!

Passo 2

Aí a gente quer o momento máximo nessa viga. Precisamos do diagrama de momento. A

Primeiro se acha as reações de apoio:

∑ M a = 0 → - 80 × 1 - 60 × 3 + 2 F b = 0

F b = 130 k N

∑ F y = 0 → F a + 130 - 80 - 60 = 0

F a = 10 k N

Passo 3

Agora, vamos fazer o diagrama de momento fletor para ver como o momento varia. A gente vai dividir nossa viga no intervalo onde há carga distribuída e onde não há e achar as equações do momento para cada intervalo.

Para o primeiro intervalo, com x originado na extremidade esquerda da viga

∑ M = 0 → M + 40 x 2 2 - 10 x = 0 → M = - 20 x 2 + 10 x

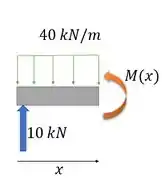
Para o segundo intervalo, com x originado na extremidade direita da viga

∑ M = 0 → - M - 60 x = M = - 60 x

Fazendo o gráfico, lembrando que essas funções tem extremidades diferentes. E que a gente usa a conveção de colocar o momento positivo na parte de baixo do gráfico.

Como podemos ver, o momento máximo vale 60kNm.

Passo 4

Temos tudo agora para montar a fórmulinha da tensão:

σ m á x = M c I

Podemos ver que o momento máximo vale 60kNm. I é o momento de inércia calculado. Quem é c ?

Cara, ele é a distância do eixo horizontal que passa pelo centroide até o ponto onde nossa tensão é calculada. A tensão vai ser máxima na extremidade da seção mais longe desse eixo.

Sendo assim:

c = a - 37 a 4 648 = 180 - 75

Então:

σ m á x = 60 × 10 6 180 - 75 59940000 = 105,11 M P a

Resposta

σ m á x = 105,11 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b .4 . 5 3 , considerando a viga composta do P r o b .4.42 .
Resolver o P r o b .4.51 , considerando a viga composta do P r o b . 4.40 .
Para a viga composta do P r o b .4.43 , determinar o raio de curvatura causado pelo momento fletor M = 50k N m .
Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de 210G P a para o aço, 150G P a para o latão e
Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de 210G P a para o aço, 150G P a para o latão e