Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 26
A viga tem um peso por unidade de comprimento. Determine a força normal interna, o esforço cortante e o momento no ponto devido ao seu peso.
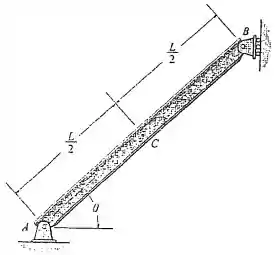
Passo 1
Para determinar o que se pede, normalmente deve-se fazer o diagrama de corpo livre de todo o corpo para que seja possível determinar alguma reação externa a um apoio, por exemplo.
Após isso, é possível apenas seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
Passo 2
Para iniciar, podemos analisar o diagrama da viga inteira, tal que:
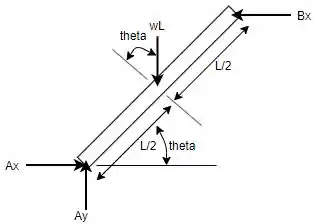
Fazendo o somatório de momentos em relação ao ponto e considerando o sentido anti-horário como positivo, tem-se:
Passo 3
Com esse resultado e cortando a viga no ponto , obtém-se a seção :
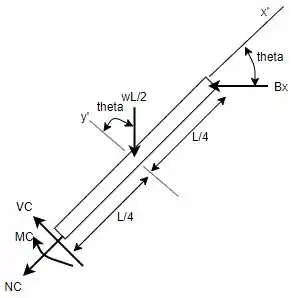
E, então, se torna possível montar as equações de equilíbrio novamente adotando um novo eixo de coordenadas.
Para o eixo , se tem:
Para o eixo :
E, novamente, considerando o sentido anti-horário como positivo, mas agora em relação ao ponto :
O sinal negativo indica que o esforço normal age no sentido oposto ao convencionado.