Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 49
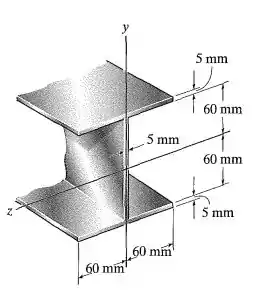
A viga tem a seção transversal mostrada na figura. Se for feita de aço com tensão admissível , determine o maior momento interno ao qual ela pode resistir se o momento for aplicado em tomo do eixo e em tomo do eixo .
Passo 1
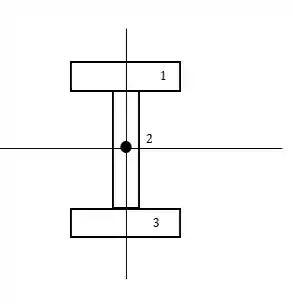
Fala aí pessoal, vamos para mais um exercício de resmat. Primeiro, vamos determinar o momento de inércia. O centro de gravidade é exatamente no meio da figura:
Portanto, seu momento de inércia em é dado por:
Para a seção , temos:
Onde é a distância para o centro de gravidade, como neste caso ela é 0, Subsitituindo:
Para as seções e , por serem simétricas, seus momentos de inércia vão ser iguais, logo:
Substituindo:
Com isso, podemos substituir no momento de inércia para o eixo . Fica assim:
Passo 2
E então, calcularmos o momento aplicado em torno do eixo através da fórmula da tensão admissional, temos:
Onde , que é a distância até a linha neutra, logo:
Passo 3
Para o momento aplicado em torno do eixo , temos:
Desta vez, o centro de gravidade é o eixo vertical na figura acima, e portando a distância das 3 seções até ela é 0. Logo:
Assim, o momento vai ser dado por:
Onde , que é a distância até a linha neutra, logo: