Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 32
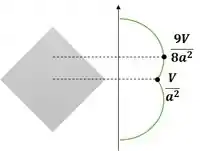
A viga tem seção transversal quadrada e está sujeita à força de cisalhamento . Faça um rascunho da distribuição da tensão de cisalhamento na seção transversal e especifique a tensão de cisalhamento máxima. Além disso, determine o local em relação ao eixo neutro onde começará a aparecer uma trinca ao longo do elemento devido ao cisalhamento.
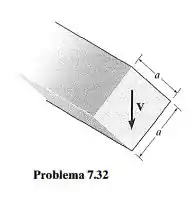
Passo 1
Vamos começar decompondo as partes de um losângulo:
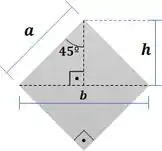
Passo 2
Agora vamos determinar o momento de inércia do losângulo. Podemos considerar o losângulo como sendo composto por dois triângulos iguais:
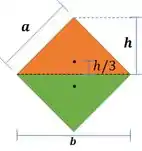
Substituíndo e
Chegamos numa expressão para o momento de inércia do losângulo.
Passo 3
O momento estático pode ser calculado considerando um triângulo:
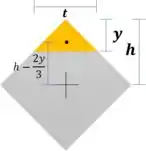
Substituíndo :
Passo 4
Aplicando tudo na equação do cisalhamento:
Simplificando o e reorganizando:
Passo 5
O ponto onde aparecerá a primeira trinca é o ponto onde a tensão de cisalhamento for máxima. Podemos encontrar esse ponto derivando a equação do cisalhamento e igualando a zero.
Mas a questão pende o ponto em relação a linha neutra.
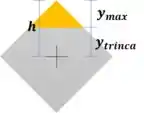
Passo 6
Agora podemos aplicar o valor e encontrar a tensão máxima
Passo 7
Para poder traçar o gráfico vamos encontrar a tensão sobre a linha do centroide, quando
Passo 8
Agora podemos traçar um gráfico, com forma parabólica, que crece até o máximo e depois decai até atingir a região do centroide. Como a seção é simétrica, o gráfico também deve ser:
