Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 131

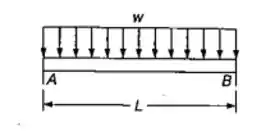
Para a viga uniforme mostrada, determinar a reação em B .  

Passo 1

Fala aí galera, bora pra mais uma questão de Resmat. Neste exercício temos uma viga bi-engastada com carga uniformemente distribuída em toda a sua extensão. Primeiro, vamos esboçar o DCL:

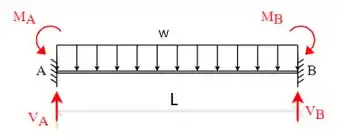
No caso de uma viga bi-engastada com carga uniformemente distribuída em toda a sua extensão, tem-se que:

R A = R B

Isso ocorre por termos uma simetria na viga. Com isso, vamos aplicar as equações de equilíbrio:

∑ F y = 0 R A + R B - w L = 0 2 R B = w L R B = w L 2

Passo 2

Em seguida, para encontrarmos os momentos é necessária uma equação de compatibilidade. Logo, a partir do apêndice D do nosso livro, encontramos as seguintes relações de rotação nos apoios:

θ B = w L 3 24 E I - M B L 3 E I - M A L 6 E I = 0

Novamente, a gente não pode esquecer da simetria que temos neste caso, portanto, temos que:

M A = M B

Substituindo:

w L 3 24 E I - M B L 3 E I - M B L 6 E I = 0 M B = w L 3 12

Resposta

R B = w L 2

M B = w L 3 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar a intensidade e a localização da maior deflexão do vão AB. Usar E = 200G P a .
Para uma viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão no ponto B. Usar E = 200 G P a .Declividade do ponto B
Para uma viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão no ponto B. Usar E = 200 G P a .Deflexão do ponto B
Para a viga com o carregamento mostrado, determinar:A reação em A
As cargas distribuídas mostradas são suportadas por pequenas vigas, que descansam sobre a viga em balanço AB. Usando E = 200G P a , determinar a declividade e a deflexão no ponto B da viga em balanço.