Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 41

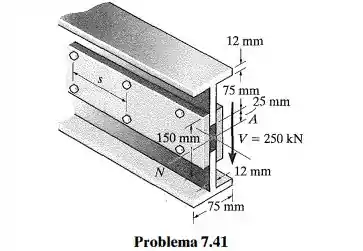
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150   m m e espessura de 12   m m . Se um cisalhamento V = 250   k N for aplicado à seção transversal, determine o espaçamento máximo dos parafusos. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN

Passo 1

Show de bolinhas galera do RespondeAí, tudo jóia com vocês?

Se liga só, esse exercício aqui nos diz que a viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150   mm e espessura de 12   mm . E sabendo que um cisalhamento V = 250   kN é aplicado a seção transversal e que cada parafuso pode resistir a uma força de cisalhamento de 75   k N , o enunciado nos pede para determinar o espaçamento máximo dos parafusos.

Belezoca, então pega a vista frontal jutamente com a vista lateral, teremos algo mais ou menos assim:

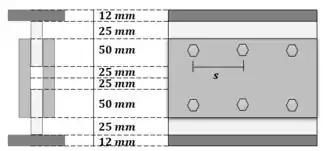
Como a maioria das questões de cisalhamento, primeiro vamos calcular as propriedades geométricas: Centroide, Momento de Inércia e Momento Estático.

Não vamos perder tempo com o centroide! A seção transversal é perfeitamente simétrica, então seu centroide é no centro.

Depois calculamos o fluxo de cisalhamento e encontramos o espaçamento entre parafusos:

Passo 2

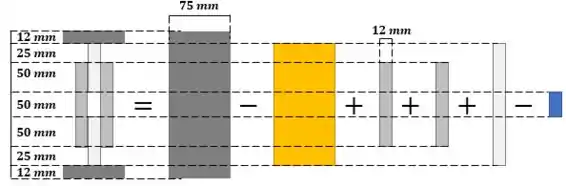
Então vamos calcular o momento de inércia em relação ao centroide. Observe a figura abaixo, vamos calcular o momento de inércia desta seção complexa por somas e subtrações de seções mais simples.

I = 75 ⋅ 224 3 12 - 75 ⋅ 200 3 12 + 2 ⋅ 12 ⋅ 150 3 12 + 12 ⋅ 200 3 12 - 12 ⋅ 50 3 12

I = 34,87 × 10 6   m m 4

Passo 3

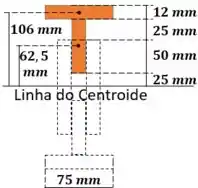
Agora vamos calcular o momento estático. Nesse caso, a melhor área é a destacada em laranja.

Q = 12 75 106 + 12 75 62,5

Q = 151650   m m 3

Passo 4

Observe a figura abaixo. Perceba que a seção que selecionamos está em contato com duas chapas laterais. Isso significa que o fluxo de cisalhamento é distribuído entre dois parafusos (um pra cada chapa). A relação entre os parafusos e fluxo de cisalhamento é:

Logo:

q = 2 F p a r a f u s o s

O número dois aparece na equação acima, pois o fluxo resiste a 2 pregos simultaneamente.

Por outro lado, a fórmula para o fluxo de cisalhamento é

q = V Q I

Igualando as duas equações:

V Q I = 2 F p a r a f u s o s

Isolando s :

s = 2 I F p a r a f u s o V Q

s = 2 × 34,87 × 10 6   m m 4 × 75   kN 250   kN × 151650   m m 3

Portanto:

s = 137,96   mm

Resposta

s = 137,96   mm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
Se a cantoneira tiver espessura de 3 m m , altura h = 100 m m e for submetida a um cisalhamento V = 50N , determine o fluxo de cisalhamento no ponto A e o fluxo de cisalhamento máximo na cantoneira.
A cantoneira está sujeita a um cisalhamento V = 10k N . Faça um rascunho da distribuição do fluxo de cisalhamento ao longo da aba AB. Indique os valores numéricos em todos os picos. A espessura é 6m m
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .