Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 93
Para virar a estrutura, um momento de binário é aplicado conforme ilustra a figura. Se a componente desse momento de binário ao longo do eixo é , determine a intensidade das forças do binário.
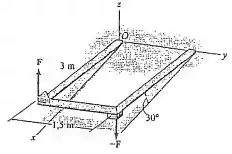
Passo 1
A questão pede para acharmos a intensidade das forças do binário sabendo que a componente do momento é . Para isso, você deve lembrar que binário é dado por
Neste caso, . Agora precisamos achar as componentes da força. Olhando no plano :
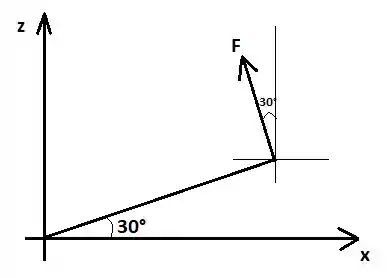
Assim, teremos
Passo 2
Desta forma, temos que
com . Fazendo o produto vetorial:
Assim, temos que
Passo 3
Desta forma, podemos igualar:
Portanto,
Assim, a intensidade da força associada ao binário é .
Resposta
Exercícios de Livros Relacionados
Determine a componente projetada da força F a b = 560 N que atua ao longo do tubo A C . Expresse o resultado como um vetor cartesiano.
Substitua o sistema de forças paralelas que age sobre a chapa por uma força resultante equivalente e especifique sua posição no plano x - z .
Substitua o sistema de forças e momentos binário que agem sobre o bloco retangular por um torsor. Especifique a intensidade da força e o momento de binário do torsor e a posição onde sua linha de ação
Se F a = 7 k NeF b = 5 k N , substitua o sistema de forças que age sobre as mísulas por uma força resultante e especifique sua posição sobre o plano x - y .
Determine as intensidades de F aeF b de modo que a força resultante passe pelo ponto O da coluna.