Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 130

Se F a = 7 k N   e   F b = 5 k N , substitua o sistema de forças que age sobre as mísulas por uma força resultante e especifique sua posição sobre o plano x - y .

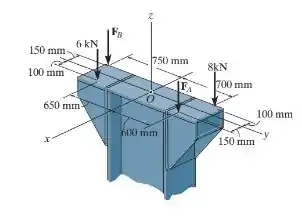
Passo 1

Desejamos substituir todas as forças indicadas na imagem por uma única força resultante e especificar onde essa força se encontra. Sendo assim, vamos tomar, primeiramente, o somatório das forças no eixo z e encontraremos

F r = ∑ F z →   - F r = - 6 - 5 - 7 - 8 → F r = 26 k N

Agora, utilizando as equações de momento podemos encontrar onde a força resultante se aplica. Dessa forma, vamos ter

M R x = ∑ M x  

→ 26 k N ⋅ y = 6 k N ⋅ 650 m m + 5 k N ⋅ 7 5 0 m m - 7 k N ⋅ 600 m m - 8 ⋅ ( 700 m m )

y = 82,7 m m

M r y = ∑ M y

→   26 x = 6 ⋅ 100 + 7 ⋅ 150 - 5 ⋅ 150 - 8 ⋅ 100

x = 3,85   m

Resposta

F r = 26 k N ,   x = 3,85 m m   e   y = 82,7 m m   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A forças F 1 e F 2 são aplicadas nas manoplas da furadeira elétrica. Substitua esse sistema de forças por uma força e momento de binário resultante equivalente agindo em O . Expresse o resultado na fo
Substitua esse sistema de forças que age sobre o encanamento por uma força e momento de binário resultante equivalente agindo em O . Expresse o resultado na forma do vetor cartesiano.
As três forças atuam no encanamento. Se F 1 = 50N e F 2 = 80N , substitua esse sistema de forças por uma força e momento de binário resultante agindo em O . Expresse o resultado na forma do vetor cart
A plataforma deve ser içada usando as três lingas mostradas. Substitua o sistema de forças que age sobre as lingas por uma força e momento de binário equivalente no ponto O . A força F 1 é vertical.
Substitua as duas forças que agem no poste por uma força e momento de binário resultante no ponto O . Expresse o resultado na forma de um vetor cartesiano.