Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 131
Determine as intensidades de de modo que a força resultante passe pelo ponto da coluna.
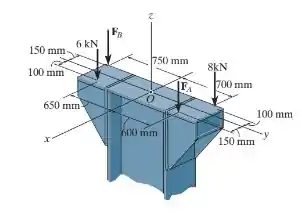
Passo 1
Desejamos encontrar o valor de e de tal forma que a força resultante passe pelo ponto , ou seja, queremos que a força resultante esteja aplicada na origem . Assim, das equações de momento obtemos
Como queremos que a nossa resultante seja aplicada na origem , teremos que o momento no eixo , aplicado pela resultante será , pois não há um braço de momento com relação ao eixo .
Assim como ocorreu no eixo , o momento da resultante no eixo também será 0.
Passo 2
Resolvendo o sistema...
Há várias formas de resolver um sistema, aqui irei multiplicar a segunda equação por 5 e somar as duas:
Obtendo...
E substituindo na equação , teremos:
E assim, terminamos mais uma questãozinha...